Diagonals of a trapezium PQRS intersect each other at the point 0 ,PQ||RS and PQ=3 RS. Find the ratio of the areas of ΔPOQ and ΔROS.
Video Solution
Text Solution
Given PQRS is a trapezium in which PQ||Rsand PQ=3 RS
⇒PQRS=31…(i)
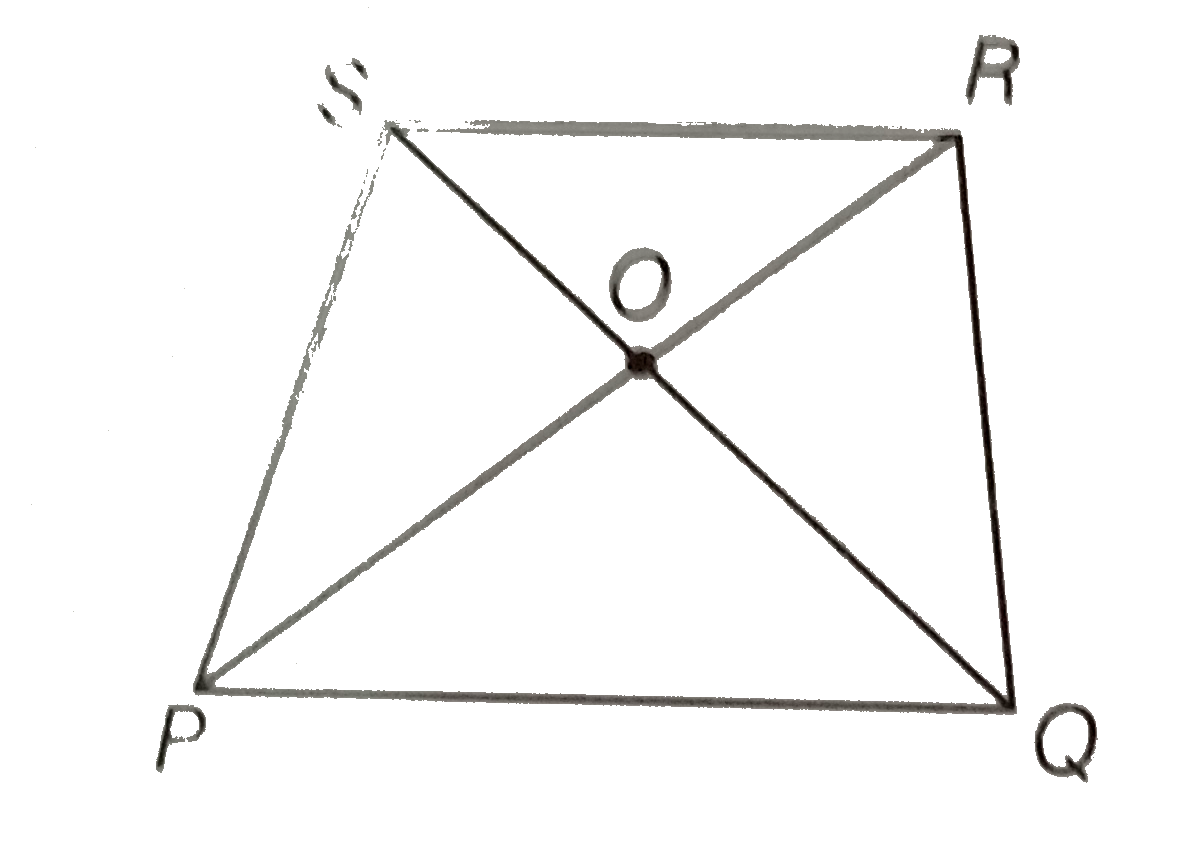
In ΔPOQ and ΔROS ∠SOR=∠QOP [vertically opposite angles]
∠SRP=∠RPQ [alternate angles]
∴ΔPOQ~ΔROS [by AAA similarity criterion]
By property of area of similar triangle,
ar(ΔPOQ)ar(ΔSOR)=(PQ)2(RS)2=(PQRS)2=(31)2 [from Eq.(i)]
⇒ar(ΔPOQ)ar(ΔSOR)=91
Hence, the required ratio is 9 : 1
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Diagonals of a Trapezium ΔBCD with AB || CD intersect each other at the point O. If AB = 2CD, then the ratio of the areas of ΔAOB and ΔCOD is
A4:1B1:16C1:4D16:1Diagonals of a quadrilateral PQRS bisect each other at right angles. If PQ = 5.5 cm, then the perimeter of PQRS is
A11cmB22cmC16.5cmD5.5(1+√2) cmABCD is a trapezium in which AB∣∣CD and AB=2CD. It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A1:2B2:1C4:1D1:4
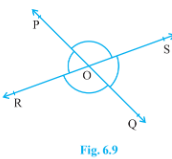
Lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, find all the angles.
View SolutionIn Fig: 6.9. lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7,find the all the angles..
View SolutionIn a trapezium ABCD, AB||DC and its digonals intersects at point O. AB = 6 cm, DC = 3 cm then find the ratio of area ΔAOBandΔCOD.
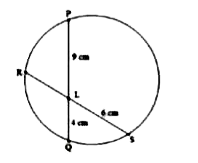
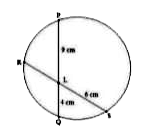
View SolutionIn the given figure, chords PQ and RS intersect each other at point L Find the length of RL.
View SolutionIn two isosceles ΔABC and ΔPQR, the ratio of sides AB : PQ is 1 : 3. Find the ratio of area of ΔABC and area of ΔPQR.
View Solution