ABCD is a trapezium in which AB||DC and P,Q are points on AD and BC respectively, such that PQ||DC, if PD=18 cm, BQ=35 cm and QC=15 cm. Find AD.
Given, a trapezium ABCD in which AB||DC. Pa nd Q are points on AD and BC, respectively such that PQ||DC. Thus, AB||PQ||DC

Join BD
In ΔABD,PO||AB [∵PQ||AB]
By basic proportionality theorem, DPAP=DOOB ....(i)
In ΔBDC,OQ||DC[∵PQ||DC]
By basic proportionality theorem,
BQQC=QBOD
⇒ (QC)/(BQ)=(OD)/(OB)......(ii)<br>FromEqs.(i)and(ii).DPAP=QCBQ
⇒18AP=1535
⇒AP=18×3515=42
∴AD+AP+DP=42+18=60cm
Topper's Solved these Questions
Similar Questions
ABCD is a trapezium in which ABIIDC and P and Qare points on AD and BC respectively such that PQ||DC. If PD= 12 cm, BQ = 42 cm and QC = 18cm, find AD.
View SolutionABCD is a trapezium in which AB || DCand P, Qare points on AD and BC respectively, such that PQ II DC. If PD - 18 cm, BQ = 35 cm and QC = 15 cm, then find the length of AD.
View Solution
Knowledge Check
ABCD is a trapizium with AB∣∣DC. E and F are points on non - parallel sides AD and BC respecitively such that EF∣∣AB, If AE = 3cm, ED = 4.8 cm, BF = 1.5 cm, then the value of CF is :
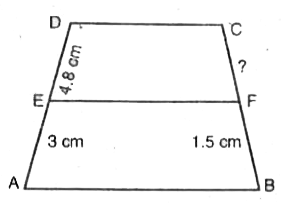 A4.5 cmB2.4 cmC6.0 cmDNone of these
A4.5 cmB2.4 cmC6.0 cmDNone of theseABCD is a trapezium of sides in which BC || AB & AB=9cm, BC=12cm, CD=15cm & DA=20cm. Find the sum of square of its diagonal.
A638B786C838D814In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cm
ABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about

View SolutionABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
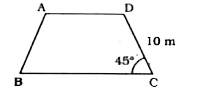
View SolutionABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=
View SolutionABCD is a kite in which AB=AD and BC= DC.
The kite is symmetrical about

View Solution
