In figure, if parallelogram ABCD and rectangle ABEM are of equal area, then

perimeter of ABCD = perimeter of ABEM
perimeter of ABCD< perimeter of ABEM
perimeter of ABCD> perimeter of ABEM
perimeter of ABCD=12 (perimeter of ABEM)
The correct Answer is:C
In rectangle ABEM, AB=EM [sides of rectangle]
and in parallelogram ABCD, CD = AB
On adding, both equations, we get
AB+CD=EM+AB ...(i)
We know that, the perpandicular distance between two parallel sides of a parallelogram is always less then the length of the other parallel sides.
∴ BE<BC and AM<AD
[since, in a right angled triangle, the hypotenuse is greater than the other sides]
On adding both above inequalities, we get
BE+AM<BC+AD or BC+AD>BE+AM
On adding AB+CD both sides, we get
AB+CD+BC+AD>AB+CD+BE+AM
⇒ AB+BC+CD+AD>AB+BE+EM+AM [∵CD=AB=EM]
∴ Perimeter of parallelogram ABCD> perimeter of rectangle ABEM
Topper's Solved these Questions
Similar Questions
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equalareas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View SolutionParallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
View Solution
Knowledge Check
In the given figure, a ||gm ABCD and a rectangle ABEF are of equal area. Then,
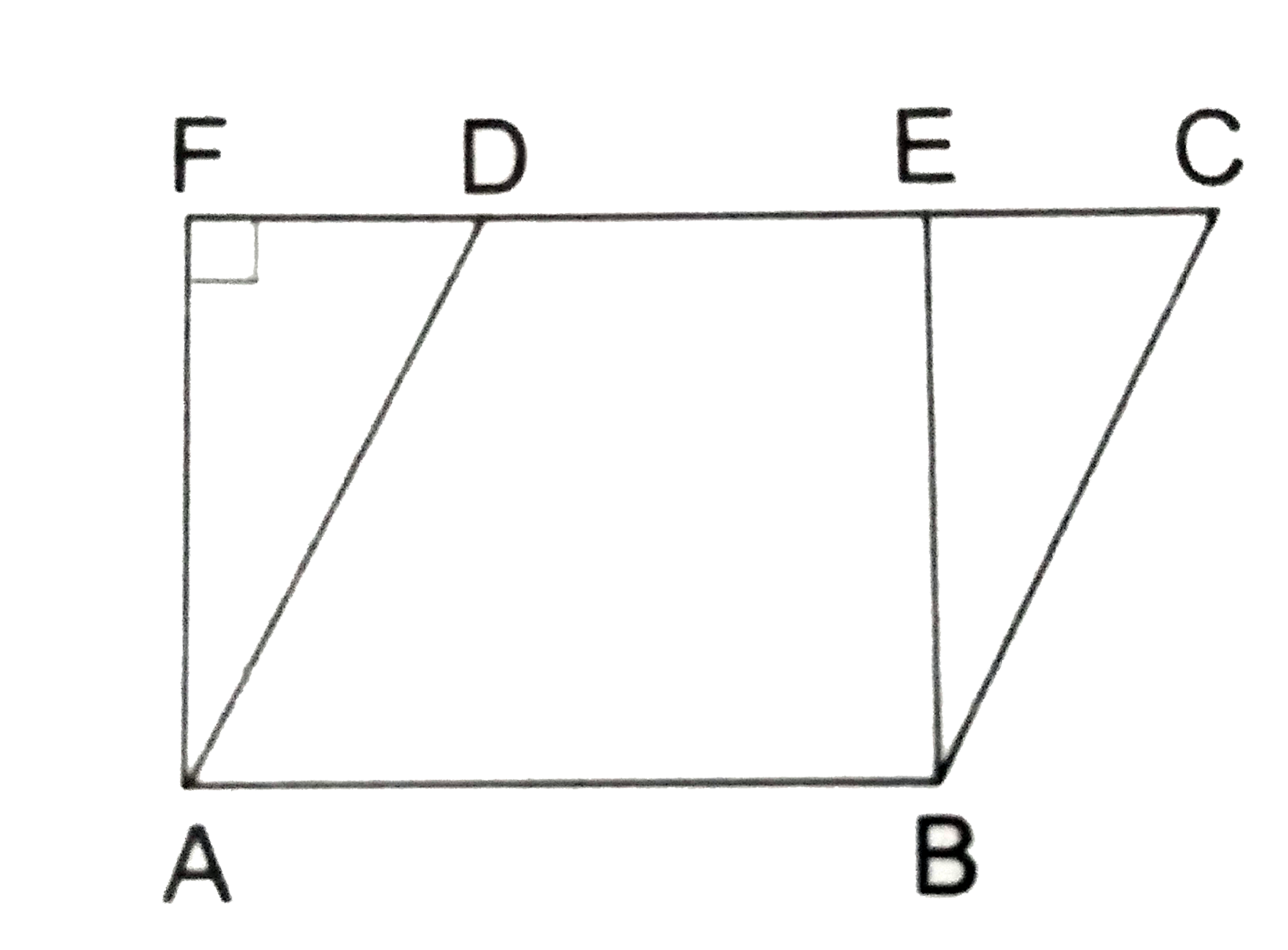 Aperimeter of ABCD = perimeter of ABEFBperimeter of ABCD < perimeter of ABEFCperimeter of ABCD > perimeter of ABEFDperimeter of ABCD =12 perimeter of ABEF
Aperimeter of ABCD = perimeter of ABEFBperimeter of ABCD < perimeter of ABEFCperimeter of ABCD > perimeter of ABEFDperimeter of ABCD =12 perimeter of ABEFIn the figure, the area of parallelogram ABCD is
 AAB×BMBBC×BNCDC×DLDAD×DL
AAB×BMBBC×BNCDC×DLDAD×DLIn given parallelogram ABCD values of x and y are equal to
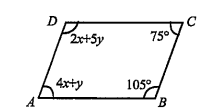 Ax=25∘,y=12.5∘Bx=12.5∘,y=25∘Cx=15∘,y=30∘Dx=15∘,y=15∘
Ax=25∘,y=12.5∘Bx=12.5∘,y=25∘Cx=15∘,y=30∘Dx=15∘,y=15∘
In the figure, ABCD is a parallelogram find value of (x+y).
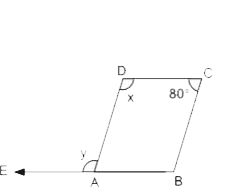
View SolutionIn the given figure, ABCD is a parallelogram. Find the area of ΔAED

View SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ

View SolutionIn a parallelogram ABCD, if ∠A=80∘ then ZB is equal to
View SolutionIn the given figure, ABCD is a parallelogram, then ∠DBAand∠BDA are respectively equal to

View Solution