O is any point inside a triangle ABC . The bisector of ∠AOB,∠BOC and ∠COA meet the sides AB,BC and CA in point D,EandF respectively. Show that ADxBExCF=DBxECxFA
To prove that AD×BE×CF=DB×EC×FA, we will use the angle bisector theorem in triangle geometry. Here’s a step-by-step solution:
Step 1: Understand the Setup
We have triangle ABC with point O inside it. The angle bisectors of angles AOB, BOC, and COA meet sides AB, BC, and CA at points D, E, and F, respectively.
Step 2: Apply the Angle Bisector Theorem
According to the angle bisector theorem:
1. In triangle AOB, since OD is the angle bisector of ∠AOB:
OAOB=ADDB
Let's call this Equation (1).
2. In triangle BOC, since OE is the angle bisector of ∠BOC:
OBOC=BEEC
Let's call this Equation (2).
3. In triangle COA, since OF is the angle bisector of ∠COA:
OCOA=CFFA
Let's call this Equation (3).
Step 3: Multiply the Ratios
Now, we will multiply the three equations obtained from the angle bisector theorem:
(OAOB)×(OBOC)×(OCOA)=(ADDB)×(BEEC)×(CFFA)
Step 4: Simplify the Left Side
On the left side, we can see that OA and OC cancel out:
1=AD×BE×CFDB×EC×FA
Step 5: Rearranging the Equation
Rearranging gives us:
AD×BE×CF=DB×EC×FA
Conclusion
Thus, we have shown that:
AD×BE×CF=DB×EC×FA
We have triangle ABC with point O inside it. The angle bisectors of angles AOB, BOC, and COA meet sides AB, BC, and CA at points D, E, and F, respectively.
According to the angle bisector theorem:
1. In triangle AOB, since OD is the angle bisector of ∠AOB:
OAOB=ADDB
Let's call this Equation (1).
OBOC=BEEC
Let's call this Equation (2).
OCOA=CFFA
Let's call this Equation (3).
Now, we will multiply the three equations obtained from the angle bisector theorem:
(OAOB)×(OBOC)×(OCOA)=(ADDB)×(BEEC)×(CFFA)
On the left side, we can see that OA and OC cancel out:
1=AD×BE×CFDB×EC×FA
Rearranging gives us:
AD×BE×CF=DB×EC×FA
Thus, we have shown that:
AD×BE×CF=DB×EC×FA
Topper's Solved these Questions
Similar Questions
XY isa line parallel to side BC of ABC.BEA and CFAB meet XY in E and F respectively.Show that ar(ABE)=ar(ACF).
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View SolutionIf O is a point in space, ABC is a triangle and D,E,F are the mid-points of the sides BC,CA and AB respectively of the triangle, prove that →OA + →OB+→OC=→OD+→OE+→OF.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
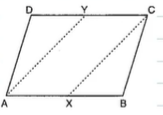
View SolutionIn Figure, ABCD is a parallelogram and X,Y are the mid=points of sides AB and DC respectively. Show that AXCY is a parallelogram.
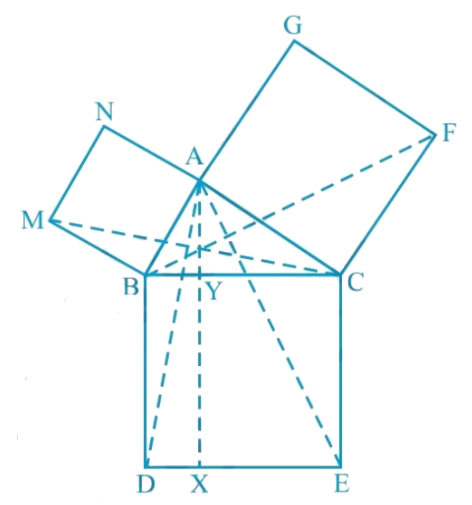
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
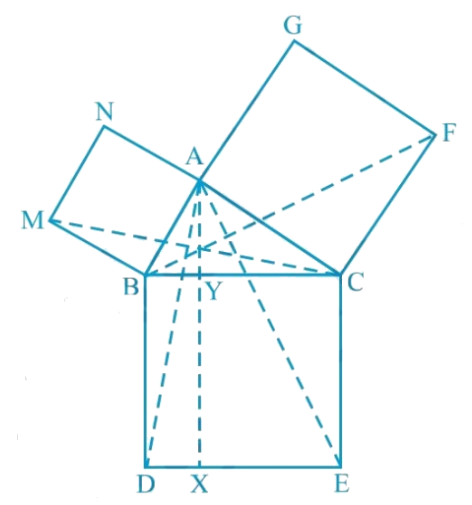
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
View SolutionIn Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
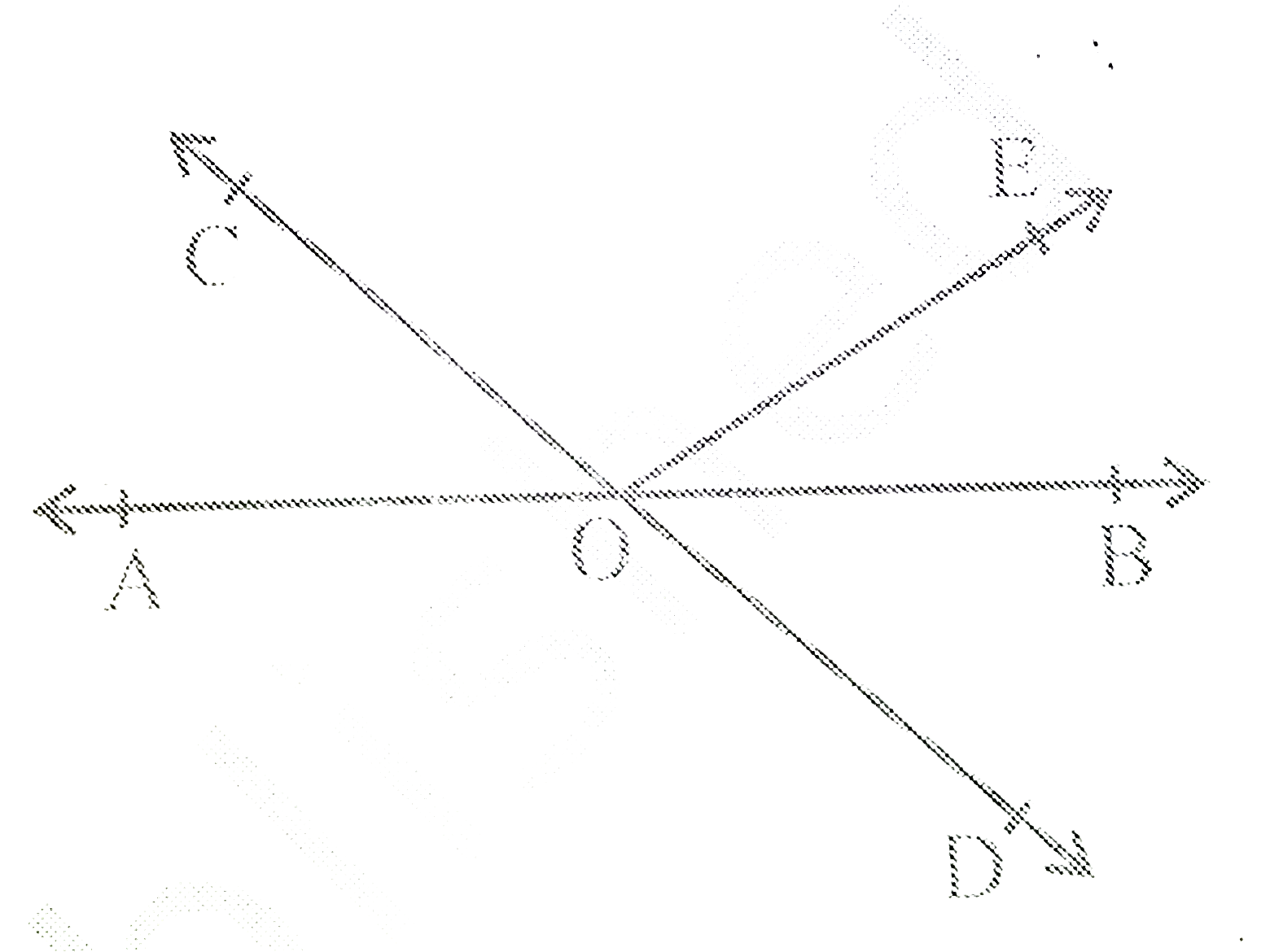
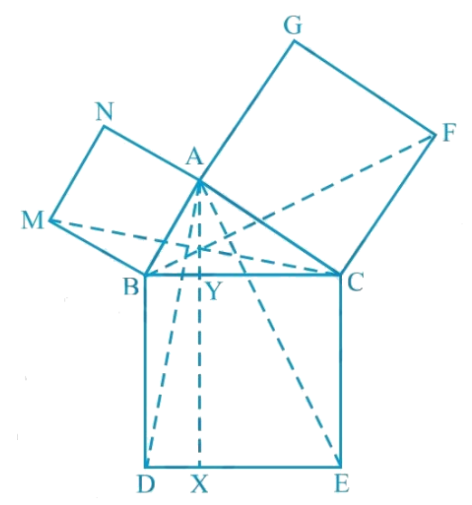
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
View Solution
