In the given figure The bisector of interior ∠A of ABC meets BC in D, and the bisector of exterior ∠A meets BC produced in E. Prove that BDBE=CDCE.
To prove that BDBE=CDCE, we will use the properties of angle bisectors in triangles.
1. Identify the Given Information:
- Let AD be the internal angle bisector of ∠A in triangle ABC, meeting BC at point D.
- Let AE be the external angle bisector of ∠A, meeting the extended line BC at point E.
2. Apply the Angle Bisector Theorem:
- According to the angle bisector theorem, for the internal bisector AD:
ABAC=BDDC(1)
- For the external bisector AE:
ABAC=BECE(2)
3. Equate the Two Ratios:
- From equations (1) and (2), we can set the two expressions for ABAC equal to each other:
BDDC=BECE
4. Cross-Multiply to Find the Required Ratio:
- Cross-multiplying gives:
BD⋅CE=BE⋅DC
- Rearranging this equation leads to:
BDBE=DCCE
- Since DC can be expressed as CD (the order of the terms does not affect the ratio), we can write:
BDBE=CDCE
5. Conclusion:
- Hence, we have proved that:
BDBE=CDCE
- Let AD be the internal angle bisector of ∠A in triangle ABC, meeting BC at point D.
- Let AE be the external angle bisector of ∠A, meeting the extended line BC at point E.
- According to the angle bisector theorem, for the internal bisector AD:
ABAC=BDDC(1)
- For the external bisector AE:
ABAC=BECE(2)
- From equations (1) and (2), we can set the two expressions for ABAC equal to each other:
BDDC=BECE
- Cross-multiplying gives:
BD⋅CE=BE⋅DC
- Rearranging this equation leads to:
BDBE=DCCE
- Since DC can be expressed as CD (the order of the terms does not affect the ratio), we can write:
BDBE=CDCE
- Hence, we have proved that:
BDBE=CDCE
Topper's Solved these Questions
Similar Questions
In the given figure The bisector of interior ∠A of ABC meets BC in D, and the bisector of exterior ∠A meets BC produced in E. Prove that BDBE=CDCE.
View SolutionThe bisector of interior ∠Aof△ABC meets BC in D, and the bisector of exterior angle ∠Ameets BC produced in E. prove that BDBE=CDCE
View Solution
Knowledge Check
In △ABC ,∠A=40∘. If the bisector of ∠B and ∠C meet at a point O in the interior of the triangle, then ∠BOC is equal to:
त्रिभुज ABC में, ∠A=40∘ है |यदि कोण B तथा कोण C के द्विभाजक त्रिभुज के आतंरिक भाग में एक बिंदु O पर मिलते हैं, तो ∠BOC का क्या होगा ?A130∘B90∘C70∘D110∘
In ABC,∠B=2∠C and the bisector of ∠B intersects AC at D. Prove that BDDA=BCBA
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionIn Figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C=1000 and ∠D=500, find the measure of ∠APB
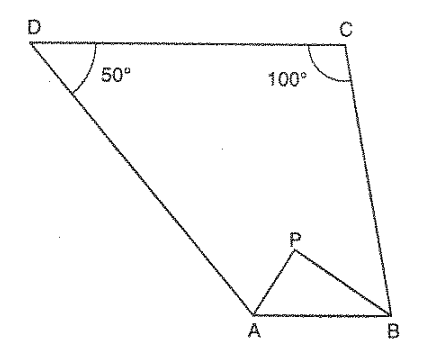
View SolutionABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
View SolutionIn figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View Solution