ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
To prove that angle D=12∠A in triangle ABC where D is the intersection of the bisector of the exterior angle at B and the bisector of angle C, we can follow these steps:
Step 1: Understand the angles involved
Let:
- ∠A=∠A
- ∠B=∠B
- ∠C=∠C
The exterior angle at B is given by:
Exterior angle at B=180∘−∠B
Step 2: Identify the angle bisectors
The bisector of the exterior angle at B divides it into two equal angles:
Angle bisector of exterior angle at B=12(180∘−∠B)=90∘−12∠B
The bisector of angle C divides it into two equal angles:
Angle bisector of C=12∠C
Step 3: Set up the angles at point D
At point D, we have:
- One angle from the bisector of the exterior angle at B: 90∘−12∠B
- One angle from the bisector of angle C: 12∠C
Step 4: Use the fact that angles around point D sum to 360∘
The angles around point D can be expressed as:
∠D+(90∘−12∠B)+12∠C=180∘
Step 5: Rearranging the equation
Rearranging gives:
∠D=180∘−(90∘−12∠B)−12∠C
∠D=90∘+12∠B−12∠C
Step 6: Substitute the angle sum property of triangle ABC
From the triangle angle sum property, we know:
∠A+∠B+∠C=180∘
Thus, we can express ∠C in terms of ∠A and ∠B:
∠C=180∘−∠A−∠B
Step 7: Substitute ∠C back into the equation for ∠D
Substituting this into our equation for ∠D:
∠D=90∘+12∠B−12(180∘−∠A−∠B)
∠D=90∘+12∠B−90∘+12∠A+12∠B
∠D=12∠A+∠B
Step 8: Simplifying further
Since ∠B is not needed in the final expression, we can isolate ∠D:
∠D=12∠A
Conclusion
Thus, we have proved that:
∠D=12∠A
Let:
- ∠A=∠A
- ∠B=∠B
- ∠C=∠C
Exterior angle at B=180∘−∠B
The bisector of the exterior angle at B divides it into two equal angles:
Angle bisector of exterior angle at B=12(180∘−∠B)=90∘−12∠B
Angle bisector of C=12∠C
At point D, we have:
- One angle from the bisector of the exterior angle at B: 90∘−12∠B
- One angle from the bisector of angle C: 12∠C
The angles around point D can be expressed as:
∠D+(90∘−12∠B)+12∠C=180∘
Rearranging gives:
∠D=180∘−(90∘−12∠B)−12∠C
∠D=90∘+12∠B−12∠C
From the triangle angle sum property, we know:
∠A+∠B+∠C=180∘
Thus, we can express ∠C in terms of ∠A and ∠B:
∠C=180∘−∠A−∠B
Substituting this into our equation for ∠D:
∠D=90∘+12∠B−12(180∘−∠A−∠B)
∠D=90∘+12∠B−90∘+12∠A+12∠B
∠D=12∠A+∠B
Since ∠B is not needed in the final expression, we can isolate ∠D:
∠D=12∠A
Thus, we have proved that:
∠D=12∠A
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a ΔABC,∠C in an obtuse angle . The bisectors of the exterior angles at A and B meet BC and AC produced at D and E respectively . If AB=AD=BE. Find ∠ACB .
A105∘B108∘C110∘D135∘
In triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionABC is a triangle. The bisectors of the internal ∠B and external ∠C intersect at D. If angle ∠BDC=50˙ , then ∠A is
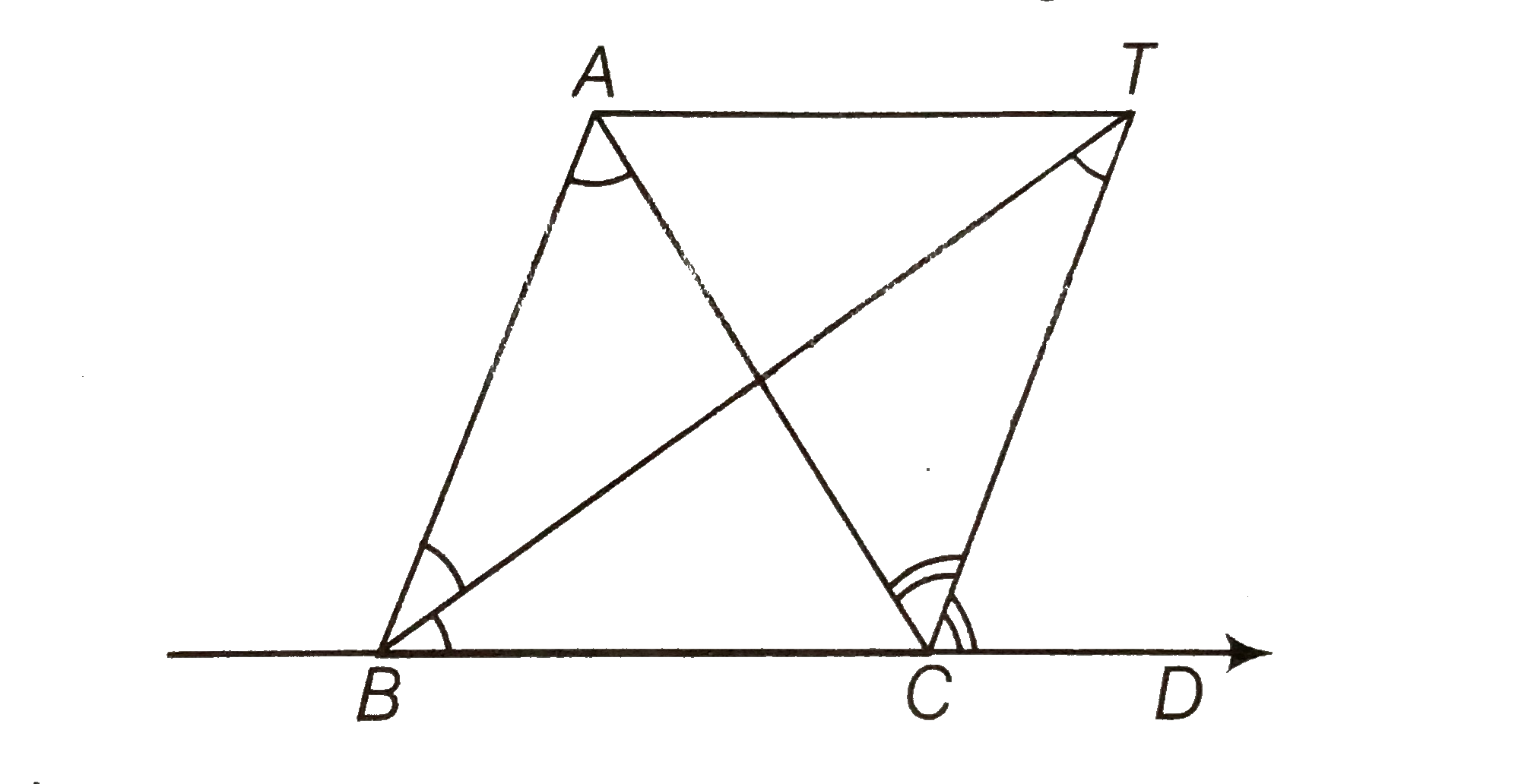
View SolutionBisectors of interior ∠B and exterior ∠ACD of a ΔABC intersect at the point T. prove that ∠BTC=12∠BAC.
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionΔABC is a right triangle right angled at A such that AB=AC and bisector of ∠C intersects the side AB at D. Prove that AC+AD=BC.
View SolutionIf in a ΔABC angle bisectors of exterior angle ∠Band∠C intersect at P ∠BPC=40∘ find ∠A
View SolutionIn a quadrilateral ABCD, CO and DO are the bisectors of ∠C and ∠D respectively. Prove that ∠COD=12(∠A+∠B)
View Solution

