Bisectors of interior ∠B and exterior ∠ACD of a ΔABC intersect at the point T. prove that ∠BTC=12∠BAC.
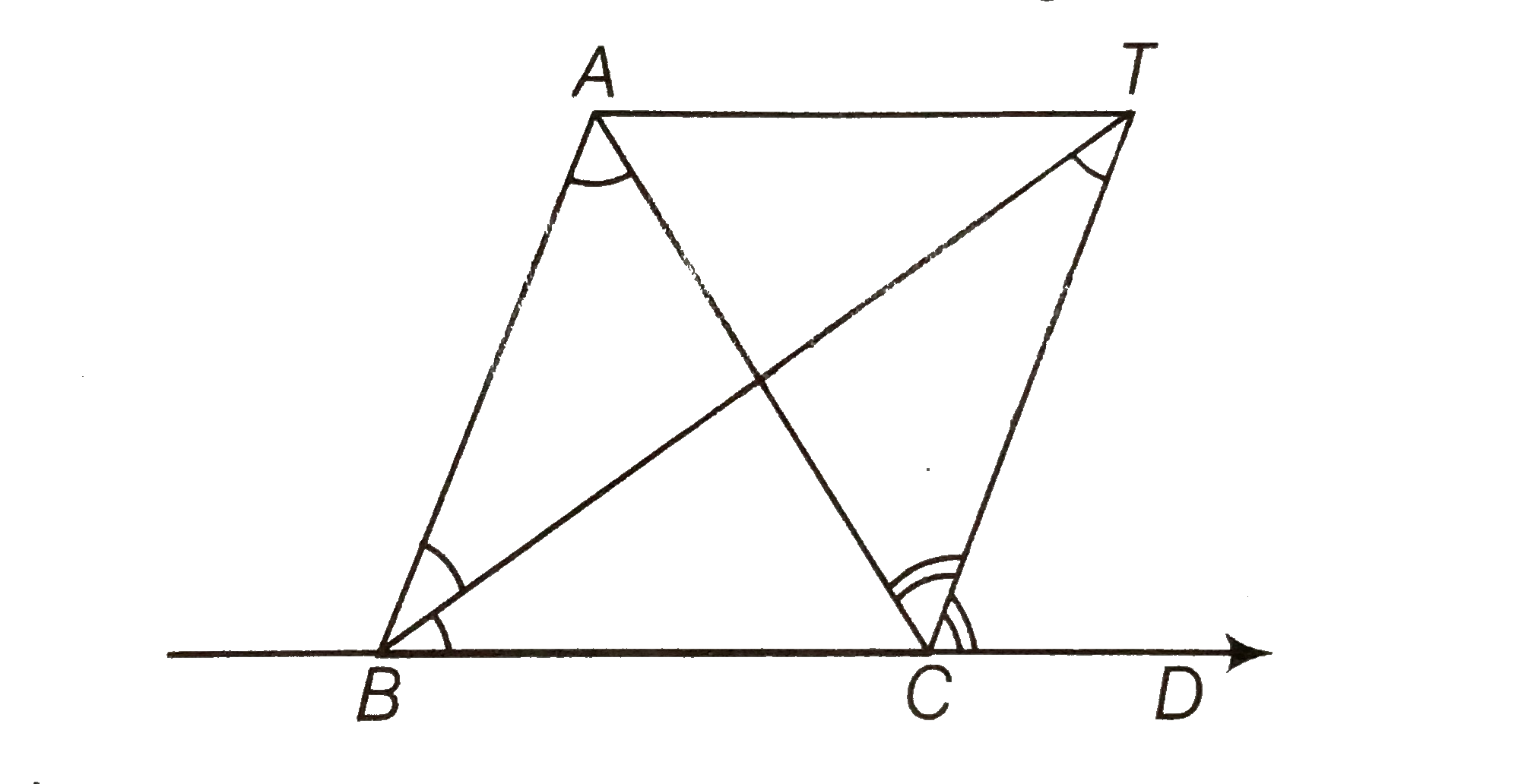
Given In Δ ABC, produce BC to DC and the bisectors of ∠ABC and ∠ACD meet at point T.
To prove ∠BTC = 1/2 ∠BAC
Proof In ΔABC, ∠C is an exterior angle.
∴ ∠ACD=∠ABC+∠CAB[exterior angle of a triangle is equal to the sum of two opposite angles]
⇒ 12∠ACD=12∠CAB+12∠ABC [dividing both sides by 2]
⇒ ∠TCD=12∠CAB+12∠ABC ....(i)
[∴CTisabisec→rof∠ACD⇒12∠ACD=∠TCD ]
In ΔBTC, ∠TCD=∠BTC+C∠CBT [exterior angles of a equal to the sum of two opposite interior angles]
⇒ ∠TCD=∠BTC+12∠ABC ....(ii) [∴BTbisectsof∠ABC⇒∠CBT=12∠ABC]
From Eqs. (i) and (ii) ,
1/2∠CAB+12∠ABC=∠BTC+12∠ABC
⇒ ∠BTC=12∠CAB
or ∠BTC=12∠ABC
Topper's Solved these Questions
Similar Questions
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D=12∠A
View SolutionThe bisectors of ∠Band∠C of an isosceles ΔABC with AB=AC intersect each other at point O. Show that the exterior angle adjacent to ∠ABC is equal to ∠BOC.
View Solution
Knowledge Check
In a ΔABC, angle bisector of interior angle B and exterior angle C intersect at P . If ∠A=70∘ . Find ∠BPC.
A25B35C40D45
In triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionThe bisectors of ∠Band∠C of an isosceles triangle with AB=AC intersect each other at a point O.BO is produced to meet AC at a point M. Prove that ∠MOC=∠ABC.
View SolutionBOandCO are bisectors of ∠B&∠C respectively of a ΔABC, intersecting each other at O. If ∠BOC=100∘ find ∠BAC.
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View SolutionIn a ABC, it is given that AB=AC and the bisectors of ∠B and ∠C intersect at O, If M is a point on BO produced, prove that ∠MOC=∠ABC.
View SolutionABC is a triangle in which the bisector of ∠B and the bisector of exterior ∠C meet at a point D such that ∠BDC=30∘. If ∠ABD=40∘, then ∠ACD and ∠BAC are, respectively, equal to
View SolutionIn a ABC, it is given that AB=AC and the bisectors of ∠B and C intersect at O. If M is a point on BO produced, prove that ∠MOC= ∠ABC
View Solution

