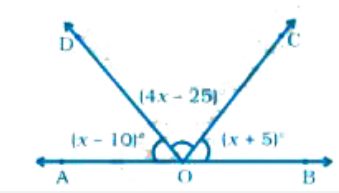
In the figure, OD is the bisector of ∠AOC, OE is the bisector of ∠BOC and OD ⊥ OE. Show that the points A, O and B are collinear. 
Video Solution
Text Solution
Given In the figure, OD ⊥OE,OD and OE and bisectors of ∠AOC and ∠BOC.
To show Points A, O and B are collinear i.e., AOB is a straight line.
Proof Since, OD and OD and OE bisect angles ∠AOC and ∠BOC, repectively.
∴ ∠AOC=2∠DOC
and ∠COB=2∠COE
On adding Equ. (i) and (ii), we get
and ∠COB=2∠COE
⇒ ∠AOC+∠COB=2∠(DOC+∠COE)
⇒ ∠AOC+∠COB=2∠DOC
⇒ ∠AOC+∠COB=2×90∘
⇒ ∠AOC+∠COB=180∘
∴ ∠AOB=180∘
So, ∠AOCand∠COB are forming linear pair.
Also, AOB is a straight line.
Hence, point A, O and B are collinear.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In △ABC ,∠A=50∘. Its sides AB and AC are produced to the point D and E. If the bisectors of the ∠CBD and ∠BCE meet at the point O, then ∠BOC will be equal to:
त्रिभुज ABC में, ∠A=50∘ है | इसकी भुजाओं AB और AC को बिंदु D तथा E तक बढ़ाया जाता है | यदि कोण CBD और कोण BCE के द्विभाजक बिंदु O पर मिलते हैं, तो ∠BOC का मान क्या होगा ?A70∘B65∘C55∘D40∘If OE is the bisector of ∠AOD in figure, then the values of x and y are respectively
 A30∘,45∘B66∘,48∘C45∘,60∘D25∘,60∘
A30∘,45∘B66∘,48∘C45∘,60∘D25∘,60∘
In Fig.20, OE is the bisector of ∠BOD. if ∠1=700, find the magnitudes of ∠2, ∠3 and ∠4.
View SolutionIn the adjoining figure, ABC is a triangle in which AD is the bisector of ∠A. If AD⊥BC, show that △ABC is isosceles.

View SolutionIn the given figure, AOB is a straight line. ∠AOC=67∘ and OD is the bisector of ∠BOC. What is the value of ∠BOD in degrees.

View SolutionIf figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.

View SolutionIn figure, ΔODC~ΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
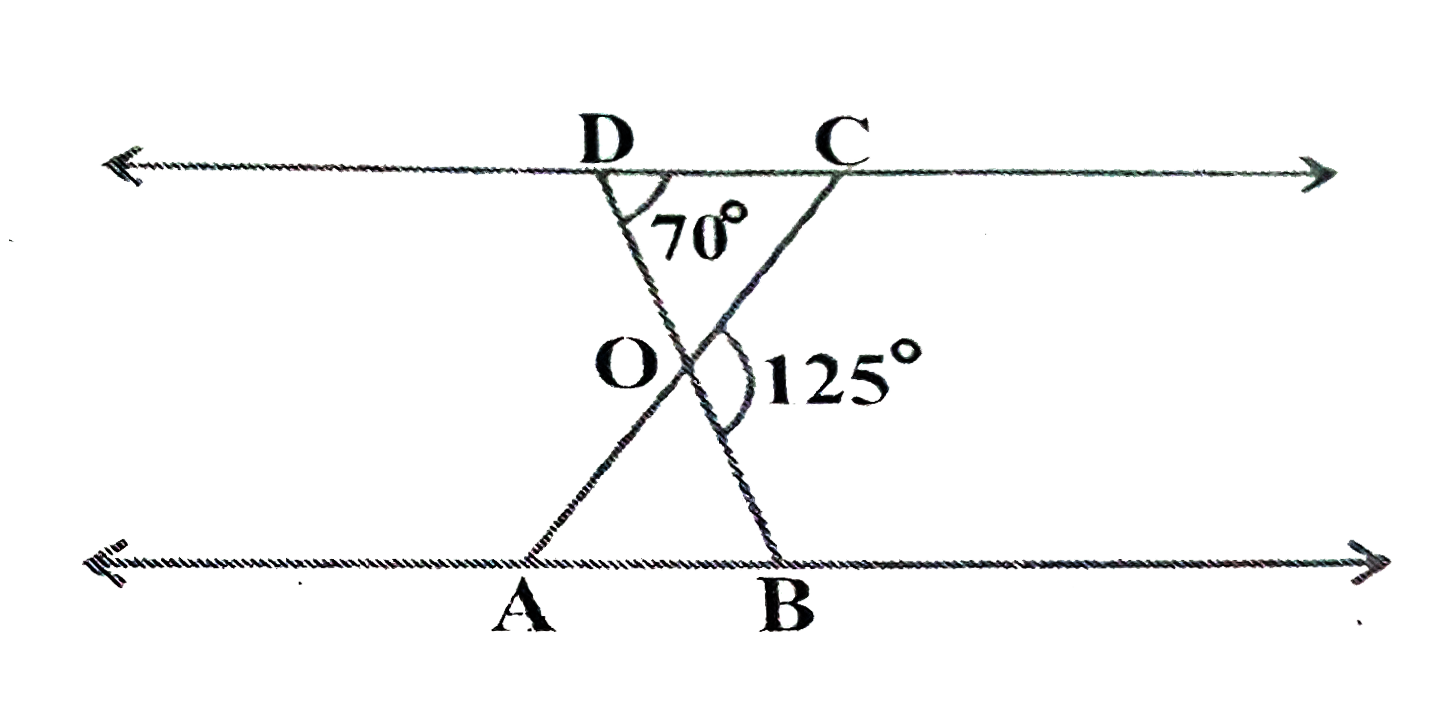
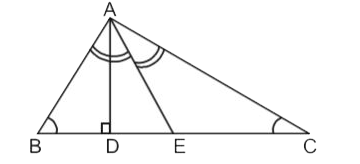
View SolutionIn the figure AE is the bisector of ∠A,AD⊥BC . Show that 2(∠ADE−∠EAC)=∠B+∠C
View Solution