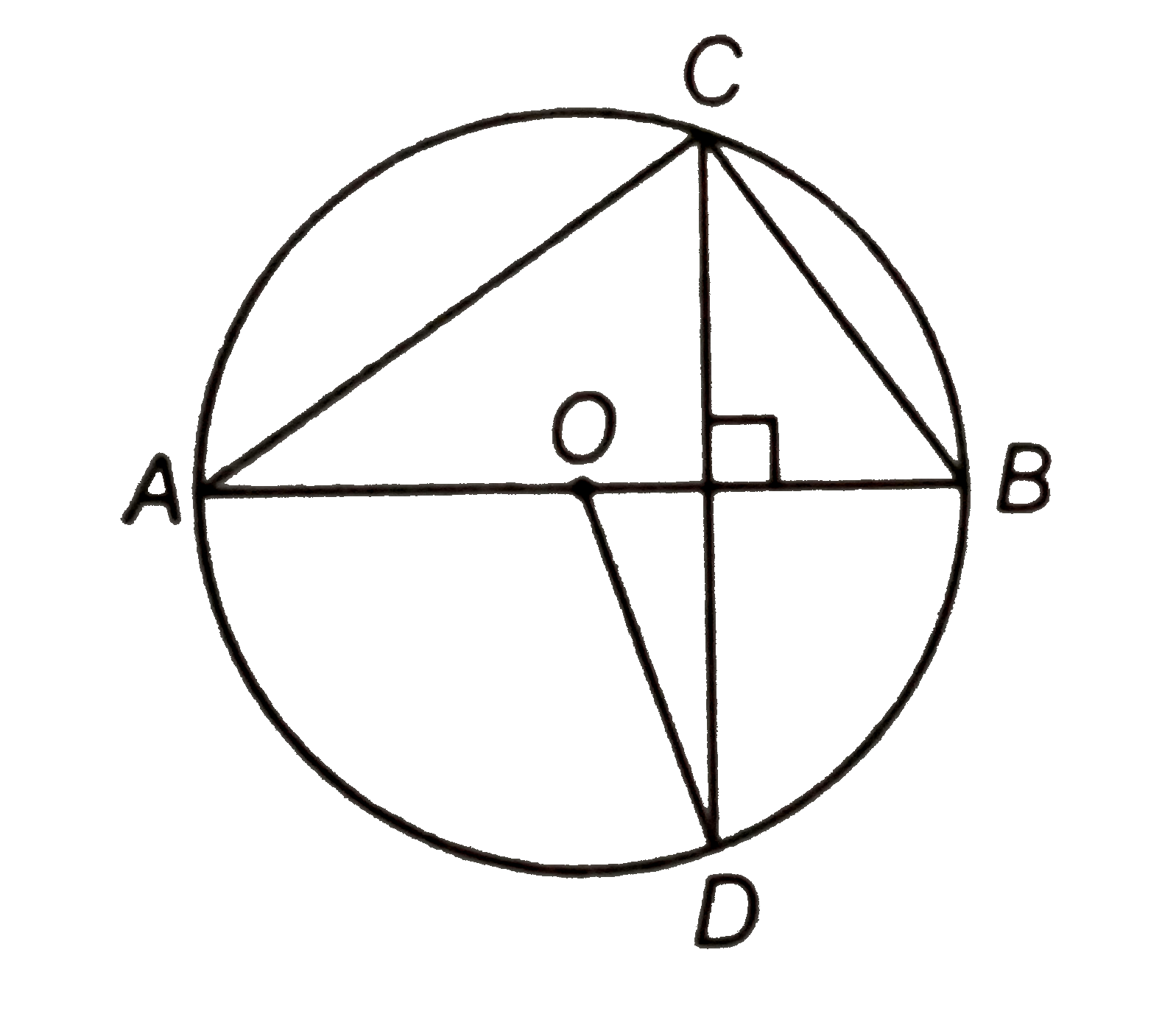
If figure, O is the centre of the circle, BD=ODandCD⊥AB. Find∠CAB.
Video Solution
Text Solution
Given, in the figureBD=OD,CD⊥AB.
In ΔOBD,BD=OD [given]
OD=OB [both are the radius of circle]
∴OB=OD=BD
Thus, ΔODB is an equilateral triangle.
∴∠BOD=∠OBD=∠ODB=60∘
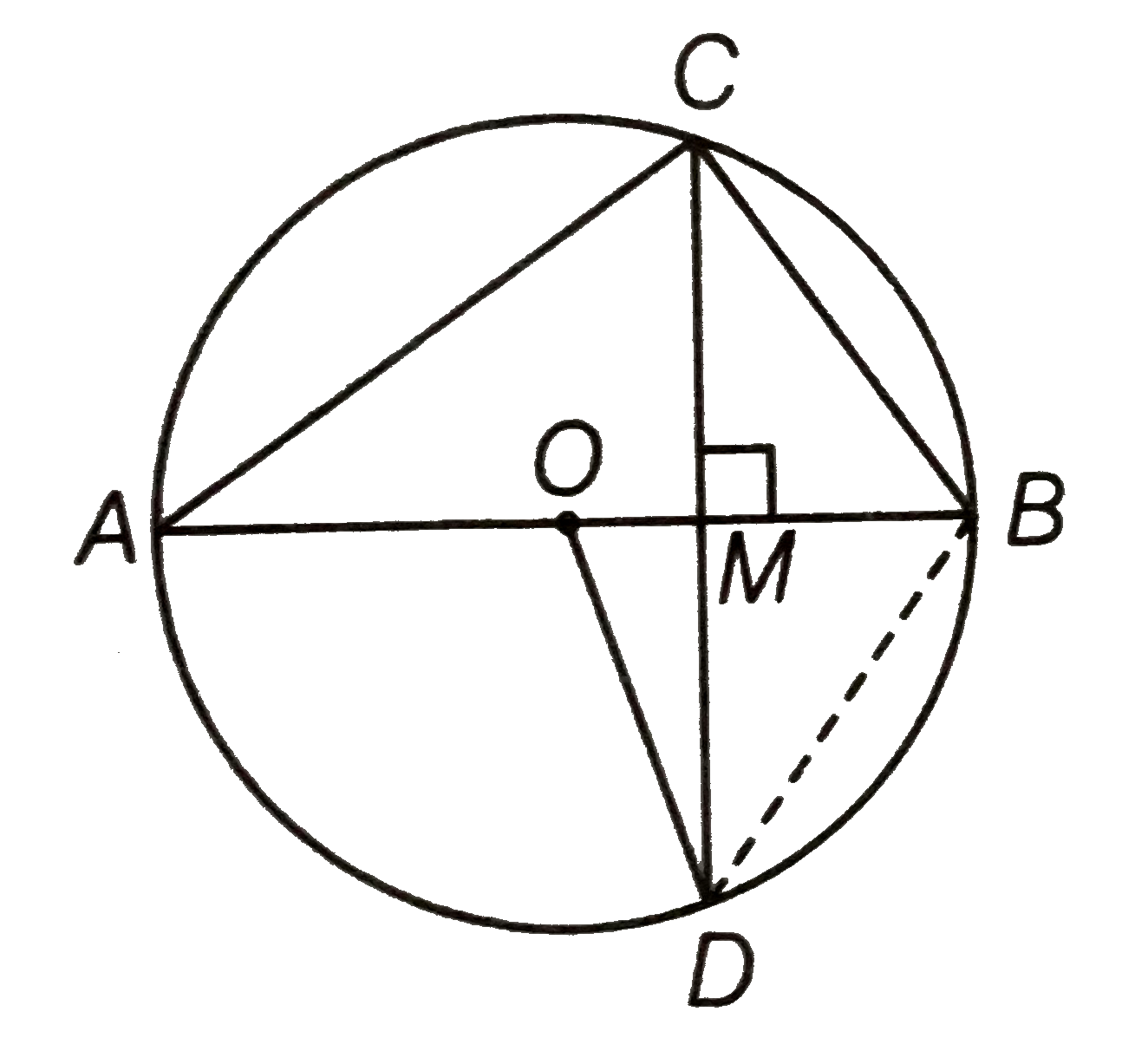
In ΔMBCandΔMBD,MB=MB [common side]
∠CMB=∠BMD=90∘
and CM=MD
[ in a circle, any perpendicular drawn on a chord also bisects the chord]
∴ΔMBC≅ΔMBD [by SAS congruence rule]
∴∠MBC=∠MBD [by CPCT]
⇒∠MBC=∠OBD=60∘[∴∠OBD=60∘]
since, AB is a diameter of the circle.
∴∠ACB=90∘
In ΔACB,∠CAB+∠CBA+∠ACB=180∘
by angle sum property of a triangle]
⇒∠CAB+60∘+90∘=180∘
⇒∠CAB=180∘−(60∘+90∘)=30∘
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.42videos
CIRCLES
- BOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles34videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
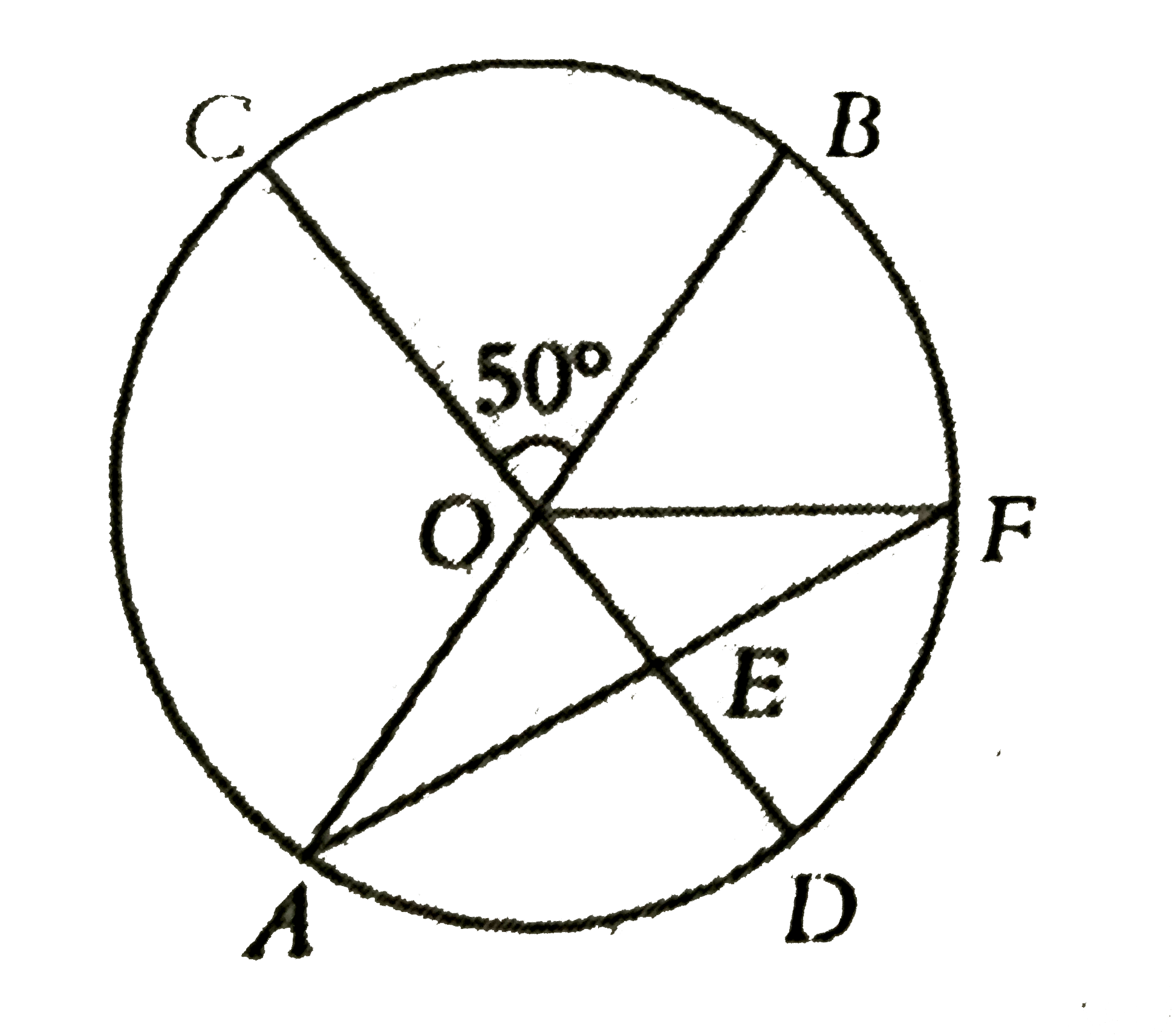
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFA130∘B100∘C110∘D120∘ - Question 2 - Select One
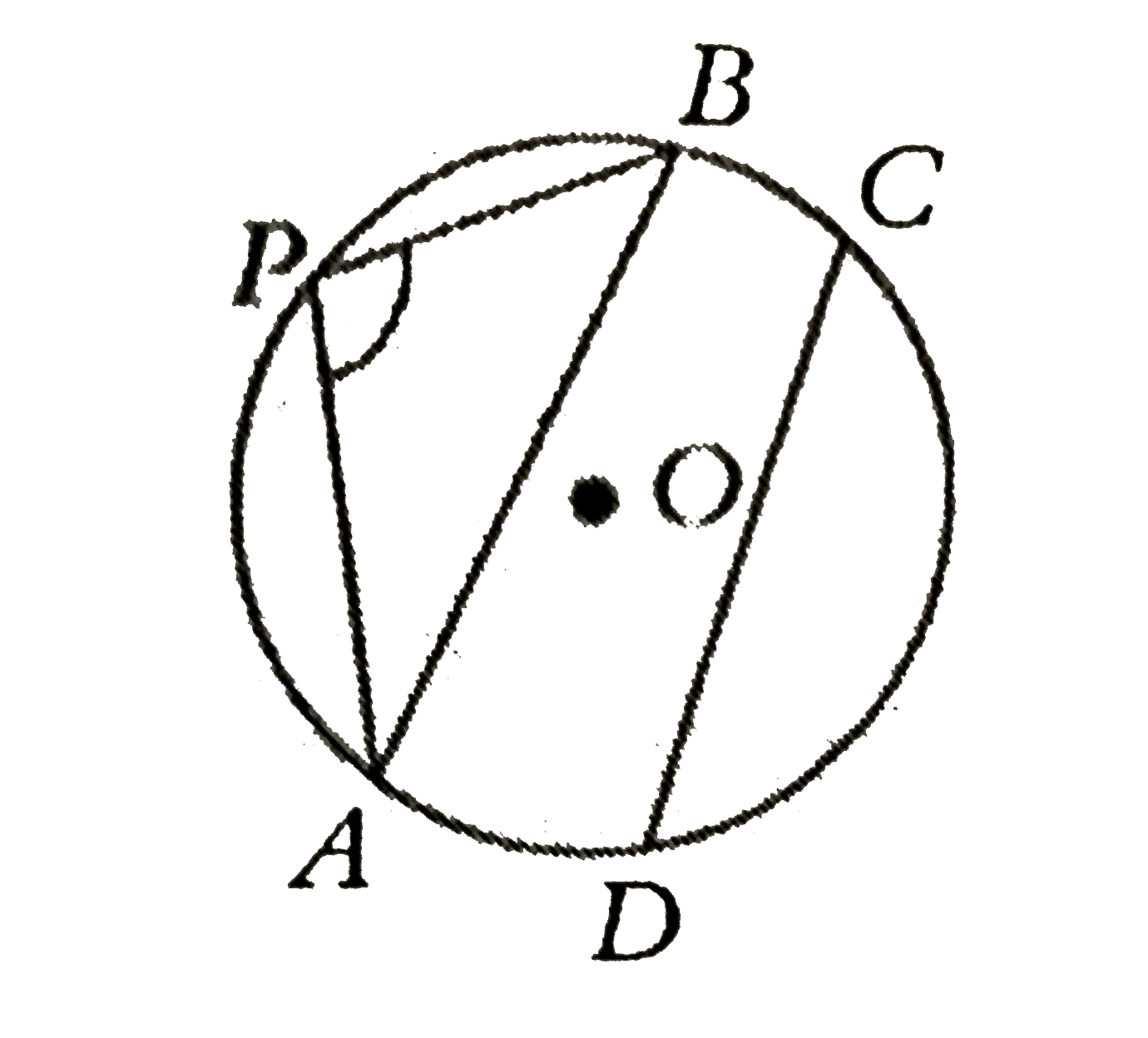
In the above figure, O is the centre of the circle and AB=CD. If ∠APB=110∘, then find the angle made by the chord CD at the centre.A220∘B110∘C120∘D140∘ - Question 3 - Select One
In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
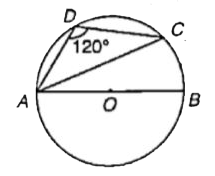 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determined

In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFView Solution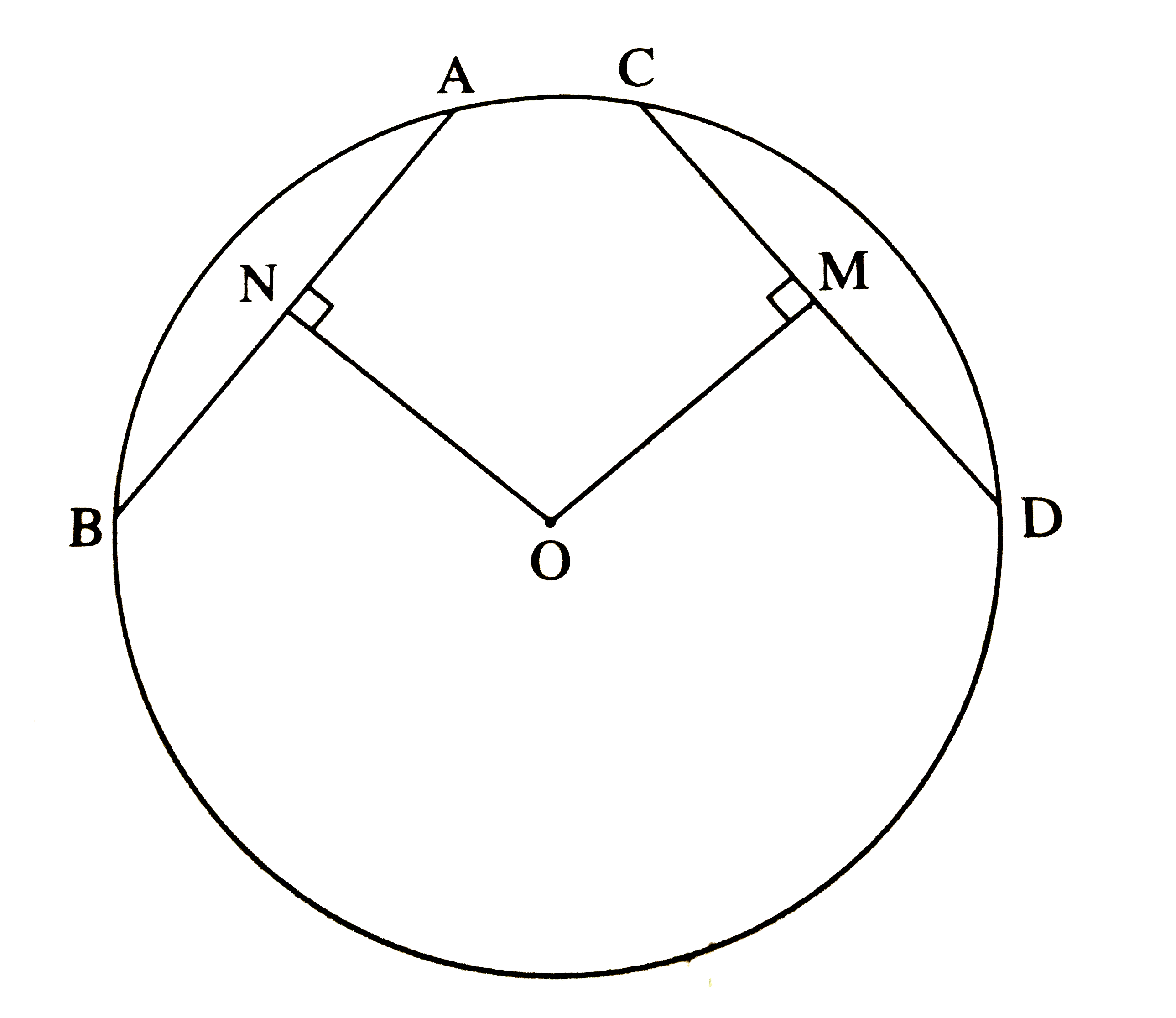
In the figure , O is the center of the circle.chord AB and CD are congruent . If seg ON ⊥ chord AB and seg OM ⊥ chord CD and OM =4cm , then find ON . Justify your answer .View SolutionIn the given figure O is the centre of the circle and AB||CD. If ∠ADC=25∘, then find ∠AEB∘-
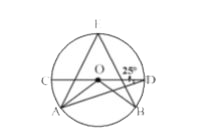 View Solution
View SolutionIn the given diagram O is the centre of the circle and CD is a tangent. ∠CABand∠ACD are supplementary to each other , ∠OAC=30∘. Find the value of ∠OCB :
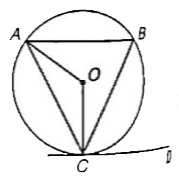 View Solution
View Solution
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.View Solution


