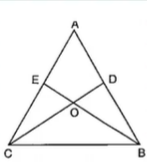
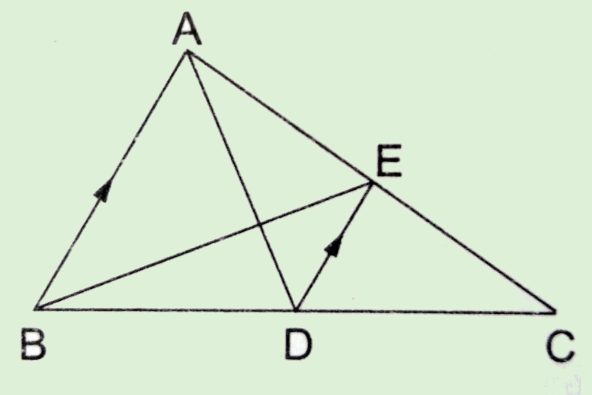
In Figure, AE bisects ∠CAD and ∠B=∠C. Prove that AE∣∣BC
Solution
In △ABC, we have
ext ∠CAD=∠B+∠C
⇒ ext.∠CAD=2∠C[∵∠B=∠C]
⇒2∠CAE=2∠C [∵ ext.'/_CADisbisectedbyAE]<br>⇒/_CAE=/_C⇒/_CAE=/_ACB=AE∥BC
Topper's Solved these Questions
Similar Questions
In Figure, it is given that AE=AD and BD=CE. Prove that AEB≅ADC
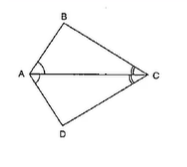
View SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE

View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD

View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
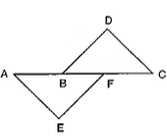
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

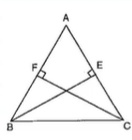
View SolutionIn Figure, BD and CE are two altitudes of a ABC such that BD=CE. Prove that ABC is isosceles.
View SolutionIn Figure, AD is the median and DE∣∣AB . Prove that BE is the median.
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
View Solution

