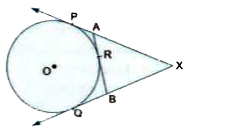
In Figure, XPandXQ are tangents from X to the circle with centre O.R is a point on the circle. Prove that, XA+AR=XB+BR
We know that the lengths of tangents drawn from a exterior point to a circle are equal.
∴XP=XQ, ………(i)[tangents from X]
AP=AR, ………(ii) [tangents from A]
BR=BQ. ………..(iii) [tangents from B]
Now, XP=XQ⇒XA+AP=XB+BQ
⇒XA+AR=XB+BR [using (ii) and (iii)].
Topper's Solved these Questions
Similar Questions
In Figure, XPandXQ are tangents from X to the circle with centre O.R is a point on the circle. Prove that, XA+AR=XB+BR
View SolutionProve that the length of the tangent drawn from an external point to a circle are equal. Using the above, do the following: TP and TQ are tangents from T to the circle with circle O and R in any point on the circle. If AB is a tangent to the circle at R, prove that TA + AR =TB +BR.

View Solution
Knowledge Check
PA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
A43∘B53∘C50∘D20∘PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
A40∘B20∘C50∘D25∘In the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
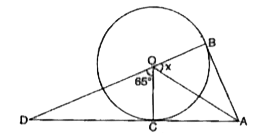 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
PA and PB are tangents to a circle with centre O from point P. OP is equal to the diameter of the circle. Prove that ABP is equilateral triangle,
View SolutionIn Fig , XP and XQ are two tangents to the circle with centre O , drawn from an external point X . ARB is another tangent, touching the circle at R . Prove that XA + AR = XB + BR.
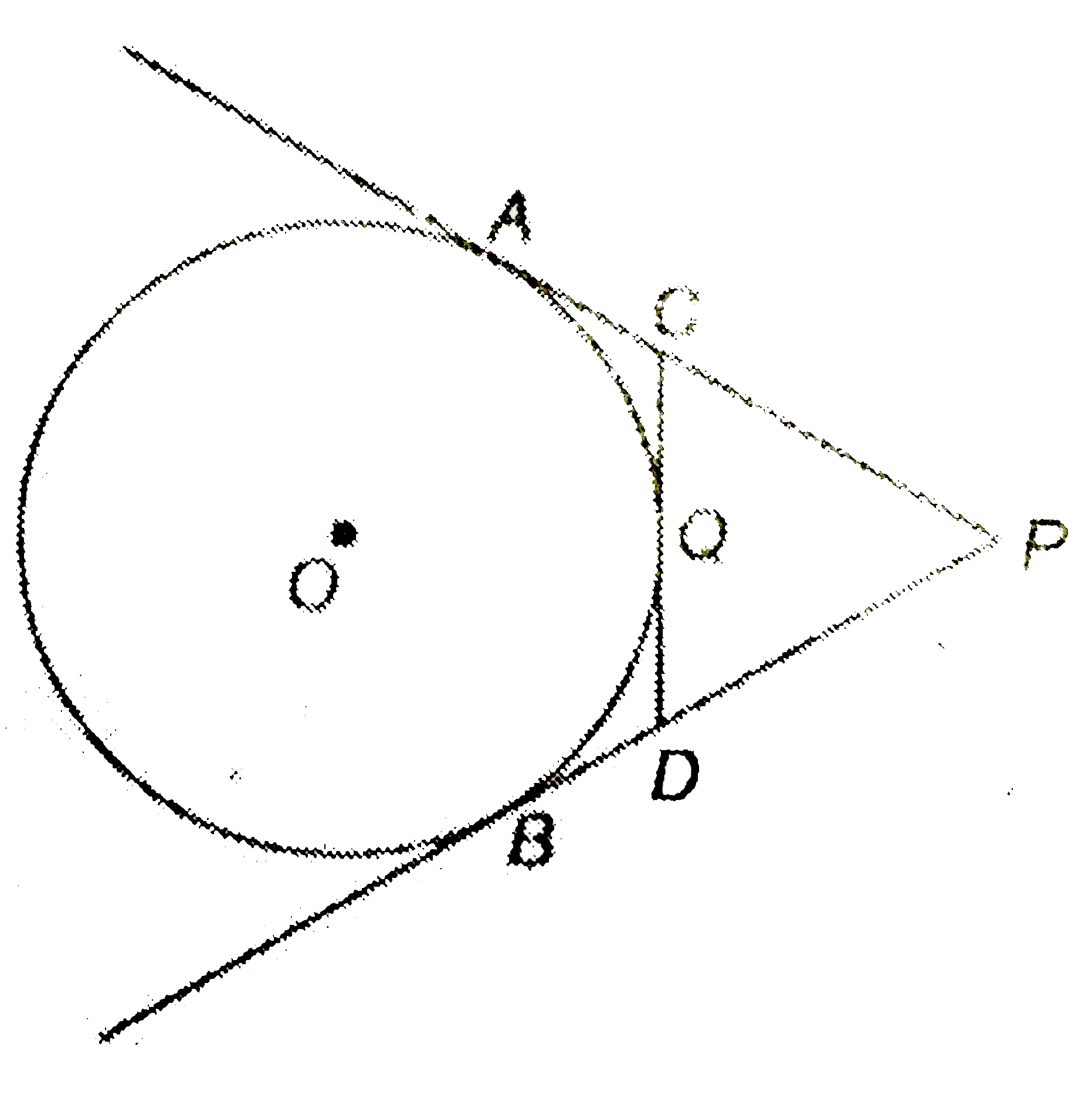
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
View SolutionPA and PB are tangents to the circle with centre O from an external point P, touching the circle at A and B respectively. Show that the quadrilateral AOBP is cyclic.
View SolutionPAandPB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN=AK+BN.
View Solution