In Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
Join OA,OC and OB
In△OCAand△OCB
OA=OB ( Radius of the circle)
∠OCA=∠OCB=900(from fig)
OC=OC (common side)
By RHS criterion of congruence
△OCA≅△OCB
∴AC=CB
Hence proved
Topper's Solved these Questions
Similar Questions
In Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
View SolutionCircles C(O, r) and C(O', r'), (r>r') touch internally at P. PQ is a chord of circle C(O, r) which intersects C(O', r') at R. Show that OO'RQ is a trapezium
View Solution
Knowledge Check
Circles C(o, r) and C(O1,r2) touch internally at a point A and AB is a chord of the circle intersecting C(O1,r2) at C. Then AC is equal to :
ACBBOACOBD13 ABTwo circles of same radius r centred at O and O' touch each other at P as shown in the figure, if OO' is produced to meet the circle C(O'r) at A and AT is a tangent to the circle C(O,r) such that O'Q ⊥ AT . Then AO : AO'=
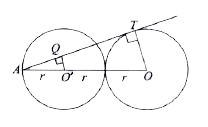 A32B2C3D14
A32B2C3D14
If O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionTwo circles C(0, r) and C(O', r') touch extemally. Show that the length of a common tangent (not through the point of contact of the circles) is 2√rr'
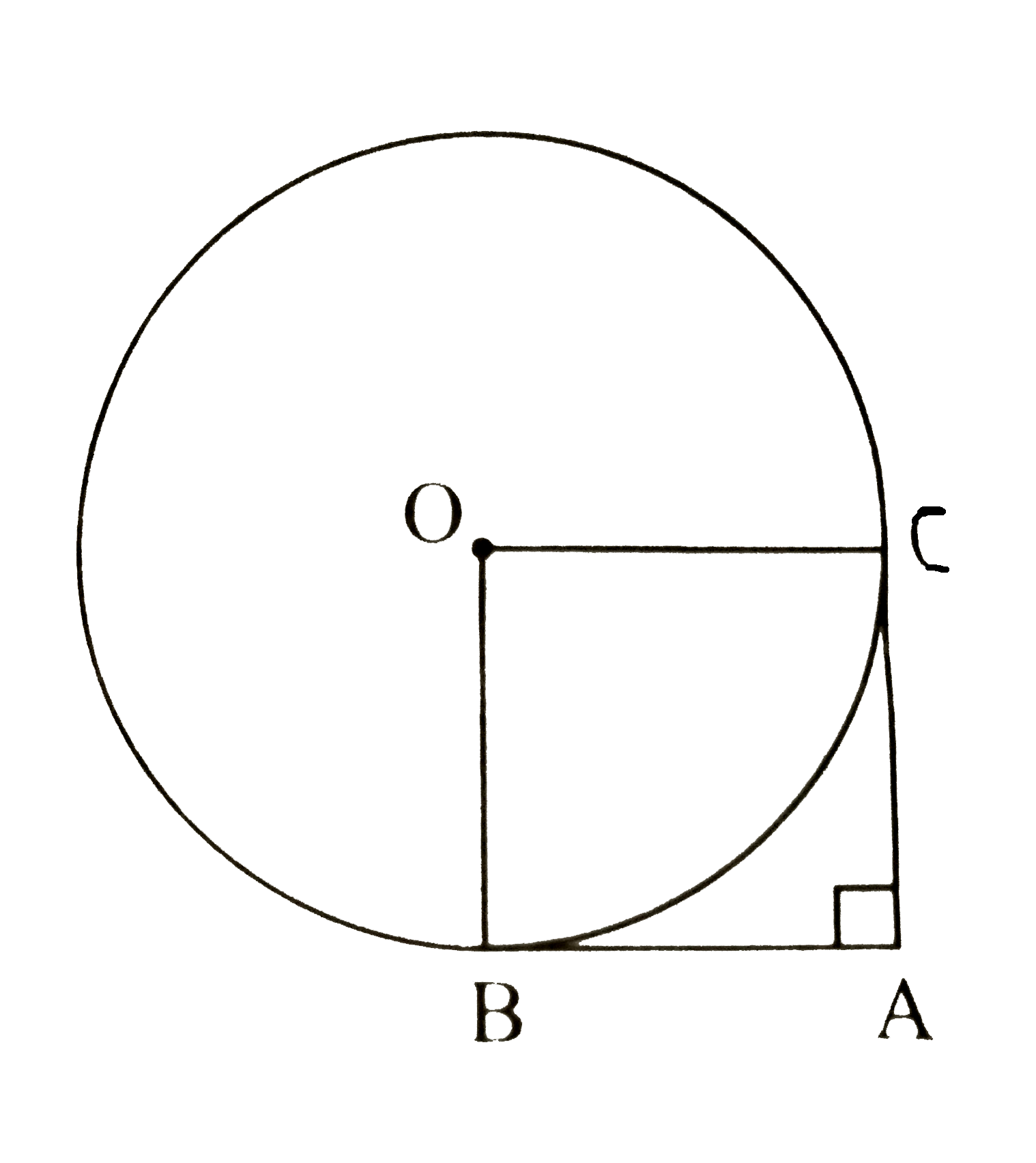
View SolutionIn the figure,tangents at B and C of the circle with centre O intersect at point A. If ∠BAC=90∘ then prove □BACO is a square
View Solution) and In this figure two bigger circles C(0,r) and C(O',r') touch each other. On third circle C(0, r) are touching the two bigger circles as well as the common tangent. Then prove
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionLet ABC be a triangle right-angled at AandS be its circumcircle. Let S1 be the circle touching the lines AB and AC and the circle S internally. Further, let S2 be the circle touching the lines AB and AC produced and the circle S externally. If r1 and r2 are the radii of the circles S1 and S2 , respectively, show that r1r2=4 area (ABC).
View Solution
