In the figure,tangents at B and C of the circle with centre O intersect at point A. If ∠BAC=90∘ then prove □BACO is a square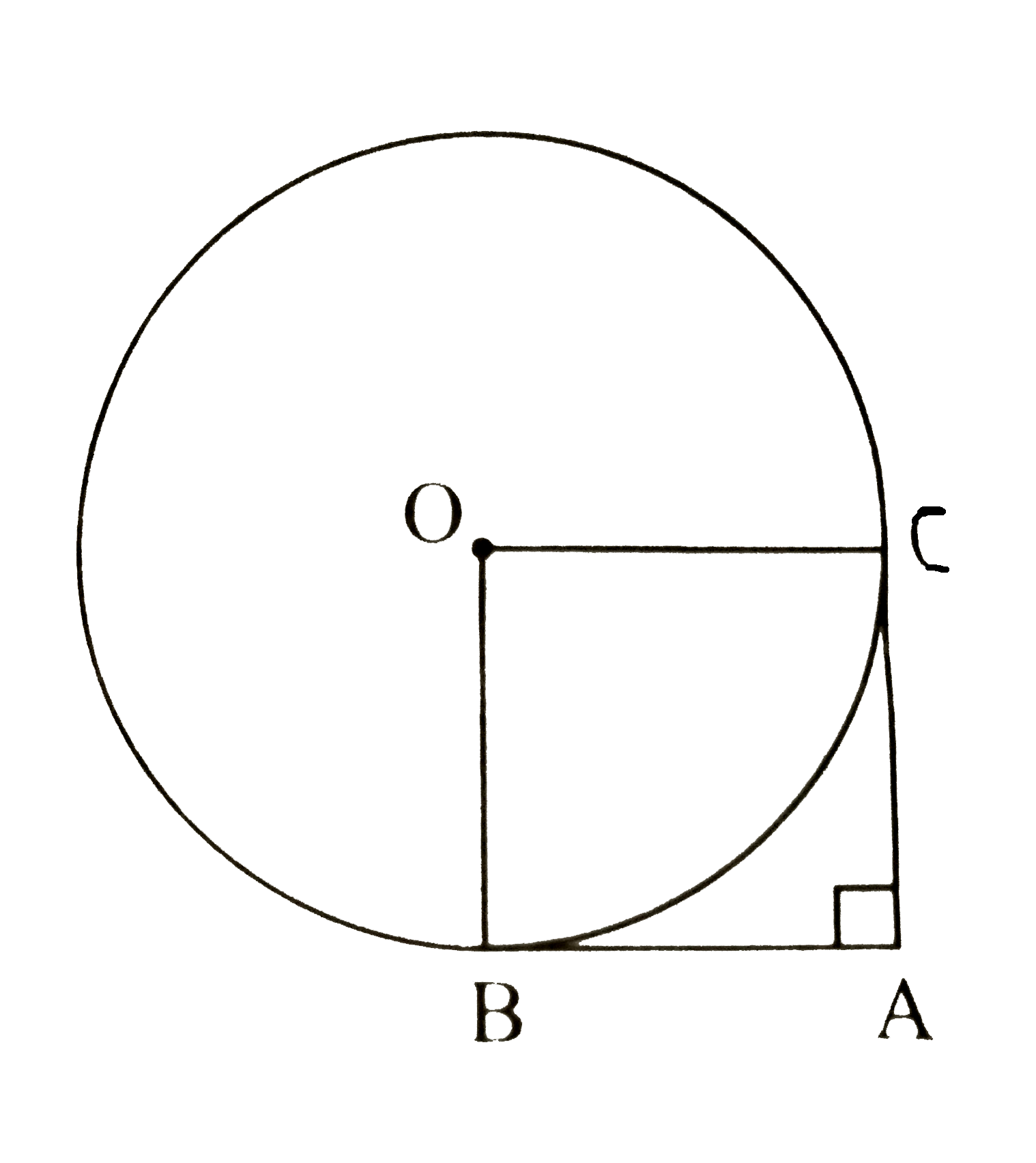 
In □BACO
∠OBA=90∘
∠OCA=90∘ ….(Tangent theorem )
∠BAC=90∘ …..(Given )
∴∠BOC90∘ ….(The sum of the measures of the angles of quadrilateral s 360∘ )
∴SquareBACO is a rectangle ....(By definition )
AB = AC ...(Tangent segments theorem )
∴□BACO is a square ...(A rectangle is a square of its adjacent sides are equal )
Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.4 (1 mark each)
9 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.5 (1 mark each)
7 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.2 (1 mark each)
9 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
In the given figure, AB and AC are tangents to the circle with centre O. Given that ∠BAC=70∘ and P is a point on the minor are BC, find ∠ BPC.
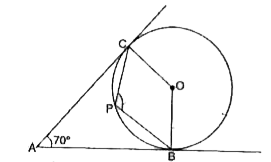A110∘B140∘C125∘D136∘
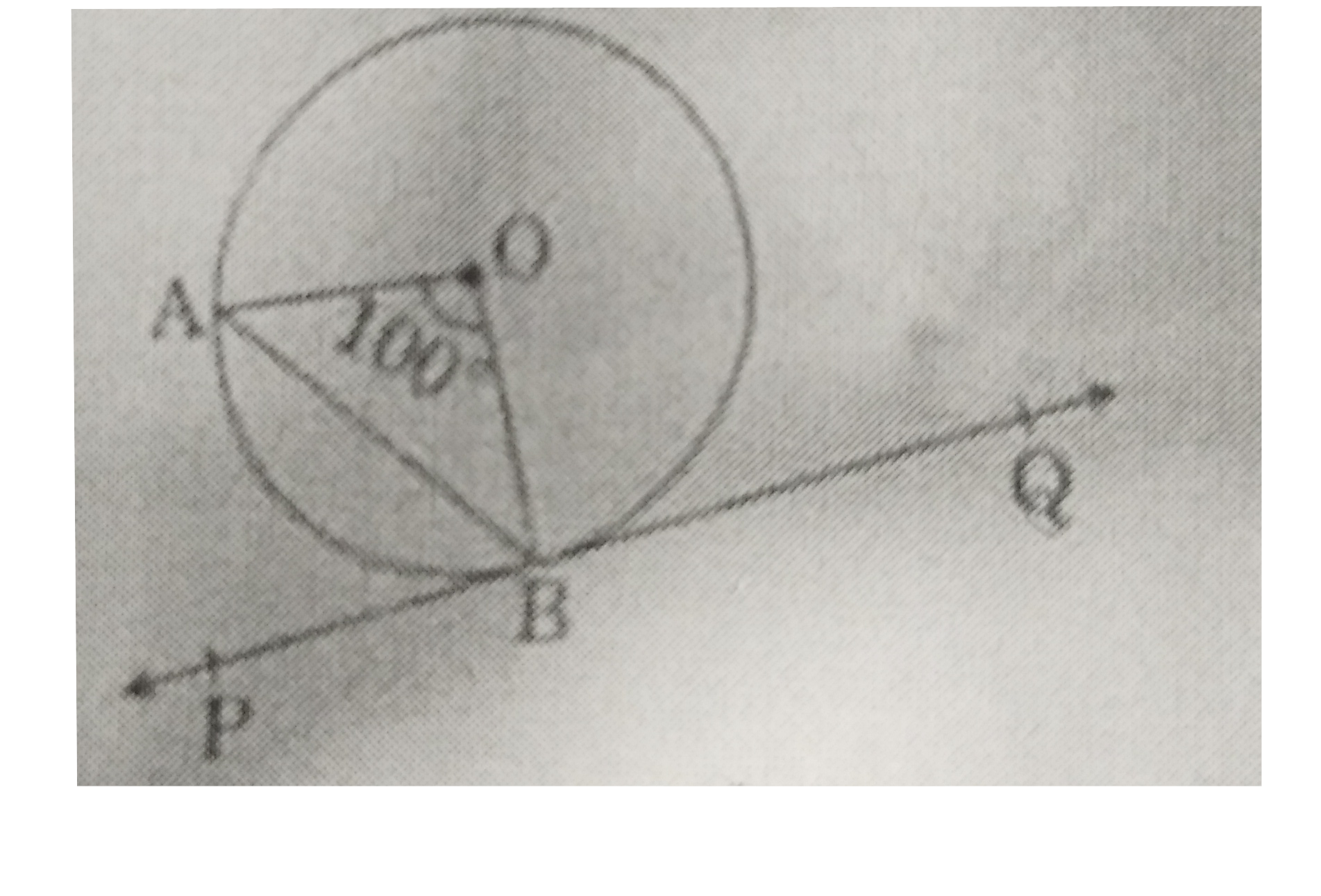
In figure-3, PQ is tangent to the circle with centre at O, at the point B. if ∠AOB=100∘, then ∠ABP is equal to
View SolutionIn Figure, two congruent circles with centers O and O' intersect at A and B. If ∠AO′B=500, then find ∠APB
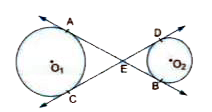
View SolutionIn Fig common tangents AB and CD to two circles with centres O1andO2 intersect at E. Prove that AB = CD.
View SolutionIn Figure, two tangents ABandAC are drawn to a circle with centre O such that ∠BAC=1200. Prove that OA=2AB
View SolutionTwo circle with centres A and B intersect at C and D. Prove that ∠ACB=∠ADB.
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
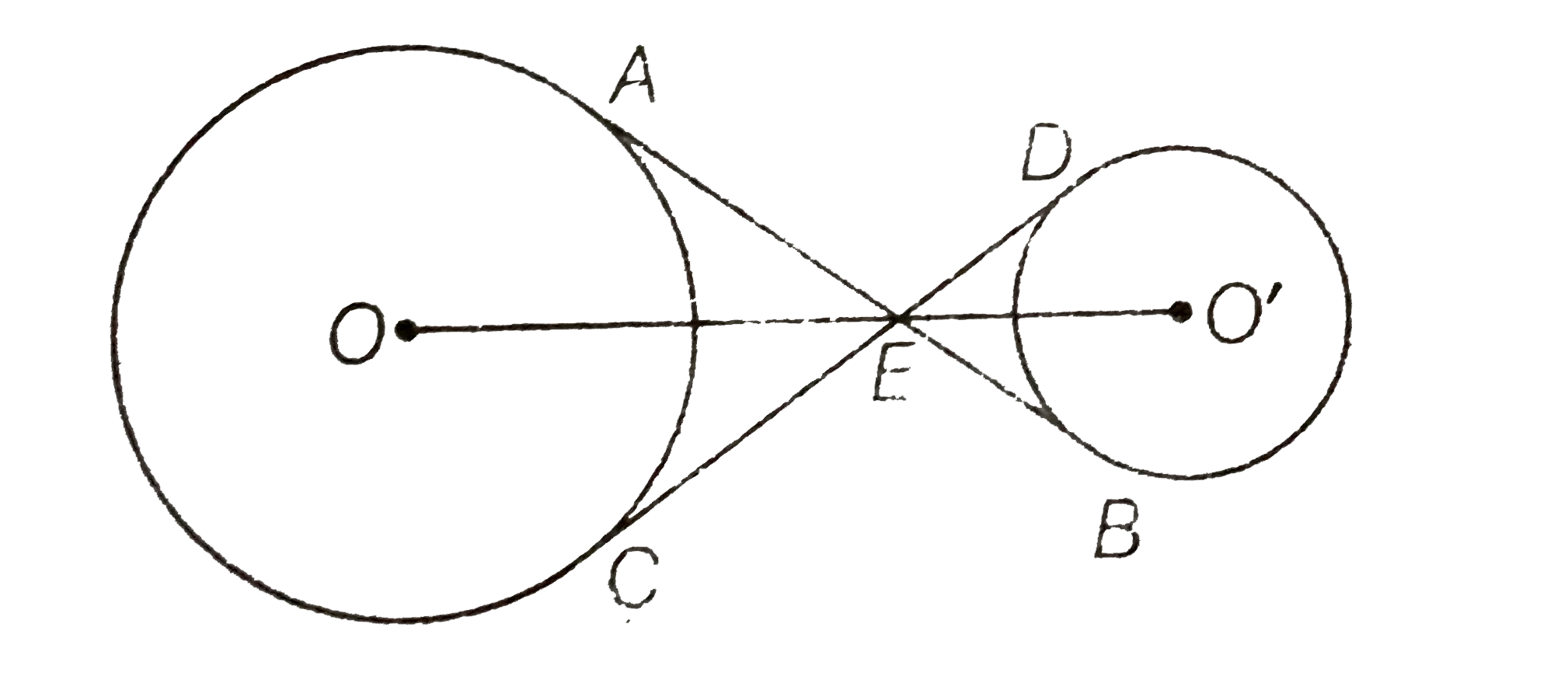
View Solution