Question

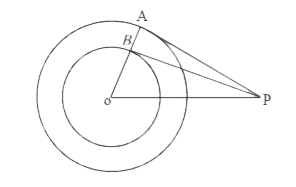
In Figure, there are two concentric circles with centre $O$
of radii $5cmand3cm$
. From an external point $P,$
tangents $PAandPB$
are drawn to these circles. If $AP=12cm,$
find the length of $BP\stackrel{.}{}$

Explanation

To solve the problem step by step, we will use the properties of tangents and the Pythagorean theorem.

Step 1: Identify the given information
- The radius of the larger circle (OA) = 5 cm
- The radius of the smaller circle (OB) = 3 cm
- The length of the tangent from point P to point A (AP) = 12 cm

Step 2: Use the Pythagorean theorem for triangle OAP
In triangle OAP, we can apply the Pythagorean theorem since OA is perpendicular to AP (the tangent at point A).

\( OP^2 = OA^2 + AP^2 \)

Substituting the known values:

\( OP^2 = 5^2 + 12^2 \)

Calculating the squares:

\( OP^2 = 25 + 144 = 169 \)

Thus,

\( OP = \sqrt{169} = 13 \text{ cm} \)

Step 3: Use the Pythagorean theorem for triangle OBP
Now, we will apply the Pythagorean theorem in triangle OBP, where OB is also perpendicular to BP.

\( OP^2 = OB^2 + BP^2 \)

Substituting the known values:

\( 169 = 3^2 + BP^2 \)

Calculating the square of OB:

\( 169 = 9 + BP^2 \)

Step 4: Solve for BP
Rearranging the equation to find BP^2:

\( BP^2 = 169 - 9 = 160 \)

Taking the square root to find BP:

\( BP = \sqrt{160} \)

Step 5: Simplify BP
We can simplify \(\sqrt{160}\):

\( BP = \sqrt{16 \times 10} = \sqrt{16} \times \sqrt{10} = 4\sqrt{10} \text{ cm} \)

Final Answer
Thus, the length of BP is \(4\sqrt{10}\) cm.

---