Circles C(O, r) and C(O', r'), (r>r') touch internally at P. PQ is a chord of circle C(O, r) which intersects C(O', r') at R. Show that OO'RQ is a trapezium
Angle included between the chord and tangent of a circle is equal to the angle in alternate segment
Also, the angle subtended by the chord at center is twice the angle in the segment of same chord
∴∠PO’R=∠POQ
But these angles are corresponding angles
∴OQ∣∣O’R
As well as QR is not parallel to OO’ (they are two distinct line having common vertex P)
Hence, quadrilateral OO’RQ is a trapezium
Topper's Solved these Questions
Similar Questions
In Figure, circle C(O,r)andC(O′r2) touch internally at a point. AandAB is a chord of the circle C(O,r) intersecting C(O′,r2) at C . Prove that AC=CB
View SolutionTwo circles C(0, r) and C(O', r') touch extemally. Show that the length of a common tangent (not through the point of contact of the circles) is 2√rr'
View Solution
Knowledge Check
Circles C(o, r) and C(O1,r2) touch internally at a point A and AB is a chord of the circle intersecting C(O1,r2) at C. Then AC is equal to :
ACBBOACOBD13 ABTwo circles of same radius r centred at O and O' touch each other at P as shown in the figure, if OO' is produced to meet the circle C(O'r) at A and AT is a tangent to the circle C(O,r) such that O'Q ⊥ AT . Then AO : AO'=
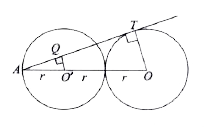 A32B2C3D14
A32B2C3D14Circles C1 and C2 of radii r and R respectively, touch each other as shown in the figure. The lime l, which is parallel to the line joining the centres of C2 and C2 is tangent to C1 at P and intersects C2 at A,B.If R2=2r2, then ∠AOB equals-
 A2212∘B45∘C60∘D6712∘
A2212∘B45∘C60∘D6712∘
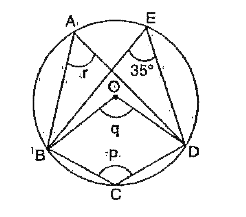
O is the centre of the circle. Find the values of p, q and r.
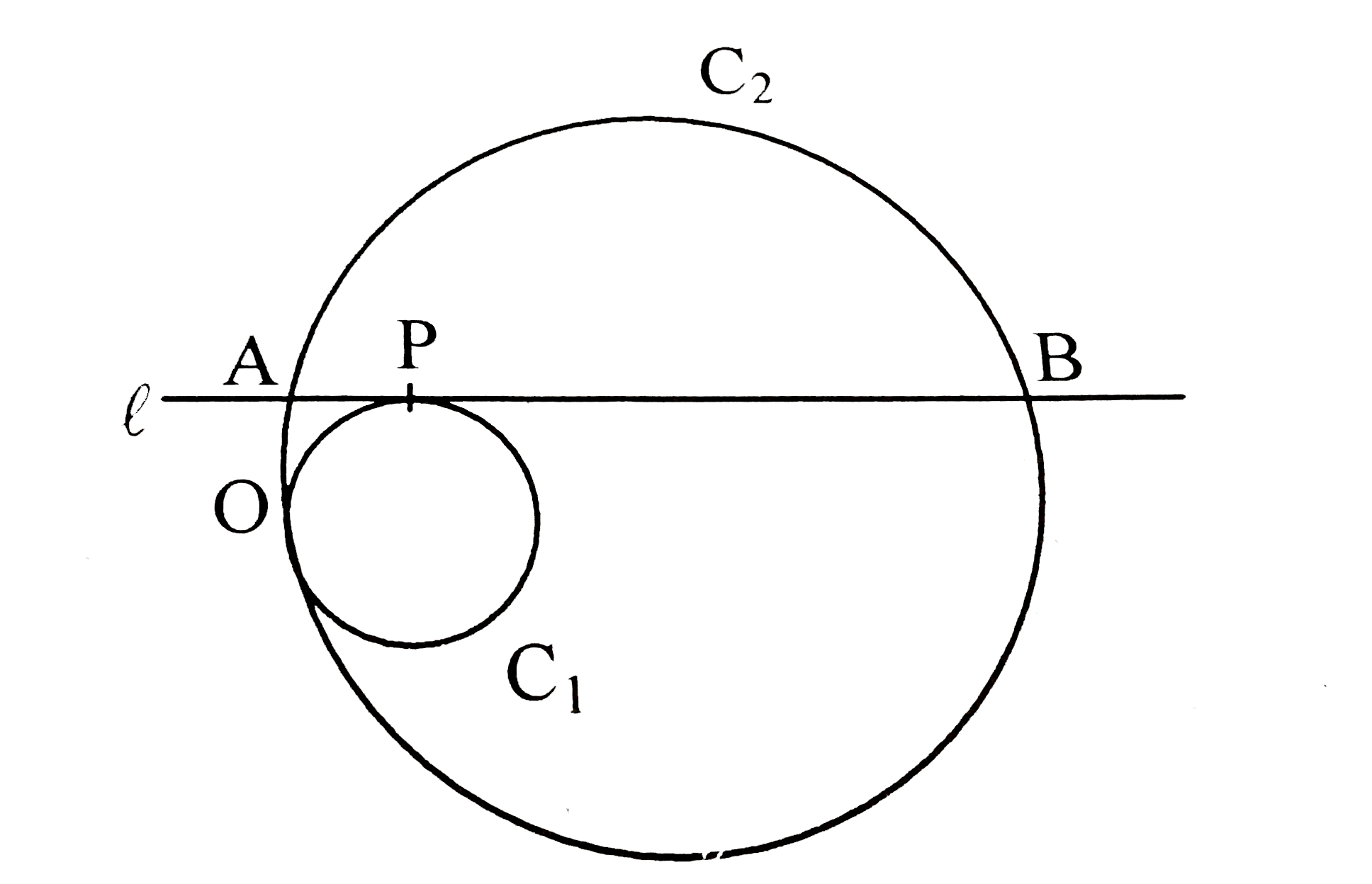
View Solution) and In this figure two bigger circles C(0,r) and C(O',r') touch each other. On third circle C(0, r) are touching the two bigger circles as well as the common tangent. Then prove
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionLet ABC be a triangle right-angled at AandS be its circumcircle. Let S1 be the circle touching the lines AB and AC and the circle S internally. Further, let S2 be the circle touching the lines AB and AC produced and the circle S externally. If r1 and r2 are the radii of the circles S1 and S2 , respectively, show that r1r2=4 area (ABC).
View Solution
