$P A$ and $P B$ are tangents to the circle with centre $O$ from an external point $P$ , touching the circle at $A$ and $B$ respectively. Show that the quadrilateral $A O B P$ is cyclic.

Video Solution

Text Solution

Verified by Experts

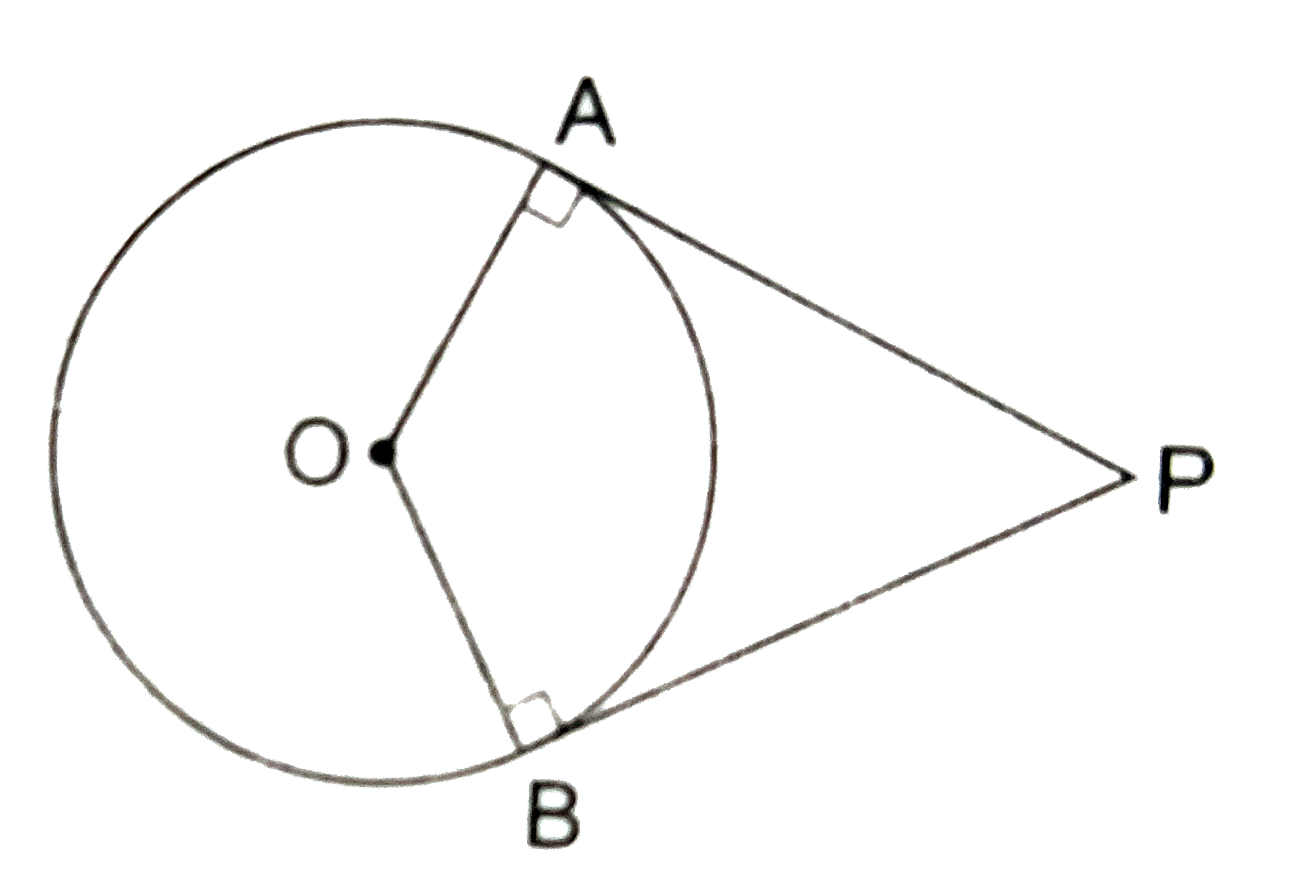
GIVEN $P A$ and $P B$ are tangents to the circle with centre $O$ from an external point $P$ .
TO PROVE Quadrilateral $A O B P$ is cyclic.
PROOF We know that the tangent at any point of a circle is perpendicular to radius through the point of contact
$∴ P A ⊥ O A$ , i.e., $∠ O A P = 90^{\circ}$ ......... $(i)$
and $P B ⊥ O B$ , i.e., $∠ O B P = 90^{\circ}$ .......... $(i i)$
Now, the sum of all the angles of a quadrilateral is $360^{\circ}$ .
$∴ ∠ A O B + ∠ O A P + ∠ A P B + ∠ O B P = 360^{\circ}$
$\Rightarrow ∠ A O B + ∠ A P B = 180^{\circ}$ [using $(i)$ and $(i i)$ ]
$∴$ quadrilateral $O A P B$ is cyclic [since both pairs of opposite angles have the sum $180^{\circ}$ ]

Updated on:21/07/2023

Two tangents PA and PB are drawn to a circle with centre O from an external point P. If $∠ O A B = 30^{\circ}$ , then $∠ A P B$ is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि $∠ O A B = 30^{\circ}$ है, तो $∠ A P B$ का मान क्या होगा ?
A $15^{\circ}$
B $30^{\circ}$
C $120^{\circ}$
D $60^{\circ}$
PA and PB are tangents to a circle with centre O, from a point P outside the circle and A and B are points on the circle. If $∠ A P B = 30^{\circ}$ , then $∠ O A B$ is equal to $:$
AA) $40^{\circ}$
BB) $15^{\circ}$
CC) $50^{\circ}$
DD) $25^{\circ}$
PA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If $∠ A P B = 40^{\circ}$ , then $∠ O A B$ is equal to:
A $40^{\circ}$
B $20^{\circ}$
C $50^{\circ}$
D $25^{\circ}$