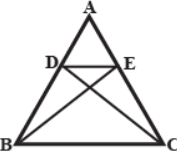
In a ABC, If LandM are points on ABandAC respectively such that LMBC. Prove that: ar(ABM)=ar(ACL)

Given
In△ABC
L is midpoint of AB
M is midpoint of AC
LM is parallel to BC
∴the area of △ on the same base and between the same parallel lines are equal
here, LM and BC are parallel
LM is the common base
∴ar(△LCM)=ar(△LBM)→eq(1)
Now, ar(△ALM) adding on both sides of eq(1)
∴ar(△ALM)+ar(△LCM)+ar(△LBM)
∴ar(△ACL)=ar(△ABM)
Topper's Solved these Questions
Similar Questions
Knowledge Check
In ΔABC, D and E are points on AB and AC respectively such that DE is parallel to BC. If AD= 2 cm, BD = 3 cm, then ar(ΔADE)ar(ΔABC) is
A49B1681C425D25
In a ABC, If LandM are points on ABandAC respectively such that LMparallelBC
Prove that: ar(LBC)=ar(MBC)
View SolutionIn a ABC , If LandM are points on ABandAC respectively such that LMparallel BC
Prove that: ar(LOB)=ar(MOC)
View SolutionIn ΔABC , if L and M are the points on AB and AC, respectively such that LM∣∣BC. Prove that ar(ΔLOB)=ar(ΔMOC).
View SolutionD and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE I I BC.
View SolutionIn Figure, D,E are points on sides AB and AC respectively of ABC, such that ar(BCE)=ar(BCD). Show that DEBC.
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionA point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View Solution
