Show that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms. GIVEN : A parallelogram ABCD.E and F are the mid-points of opposite sides AB and CD respectively. TO PROVE : ar(^(gm)AEFD)=ar(^(gm)EBCF) CONSTRCUTION : Join EF.

ABCD is a parallelogram
AB parallel CD, AB=DC
AE parallel FD and 12AB=12DC
AE parallel FD and AE=FD
∴AEFD is a parallelogram
Similarly EB=CF & EB//CF, BCEF is a parallelogram
Since parallelograms AEFD and BCEF lie on the same base and between same parallel lines
ABCD is a parallelogram
∴ar(AEFD)=ar(BCEF)
Topper's Solved these Questions
Similar Questions
Prove that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
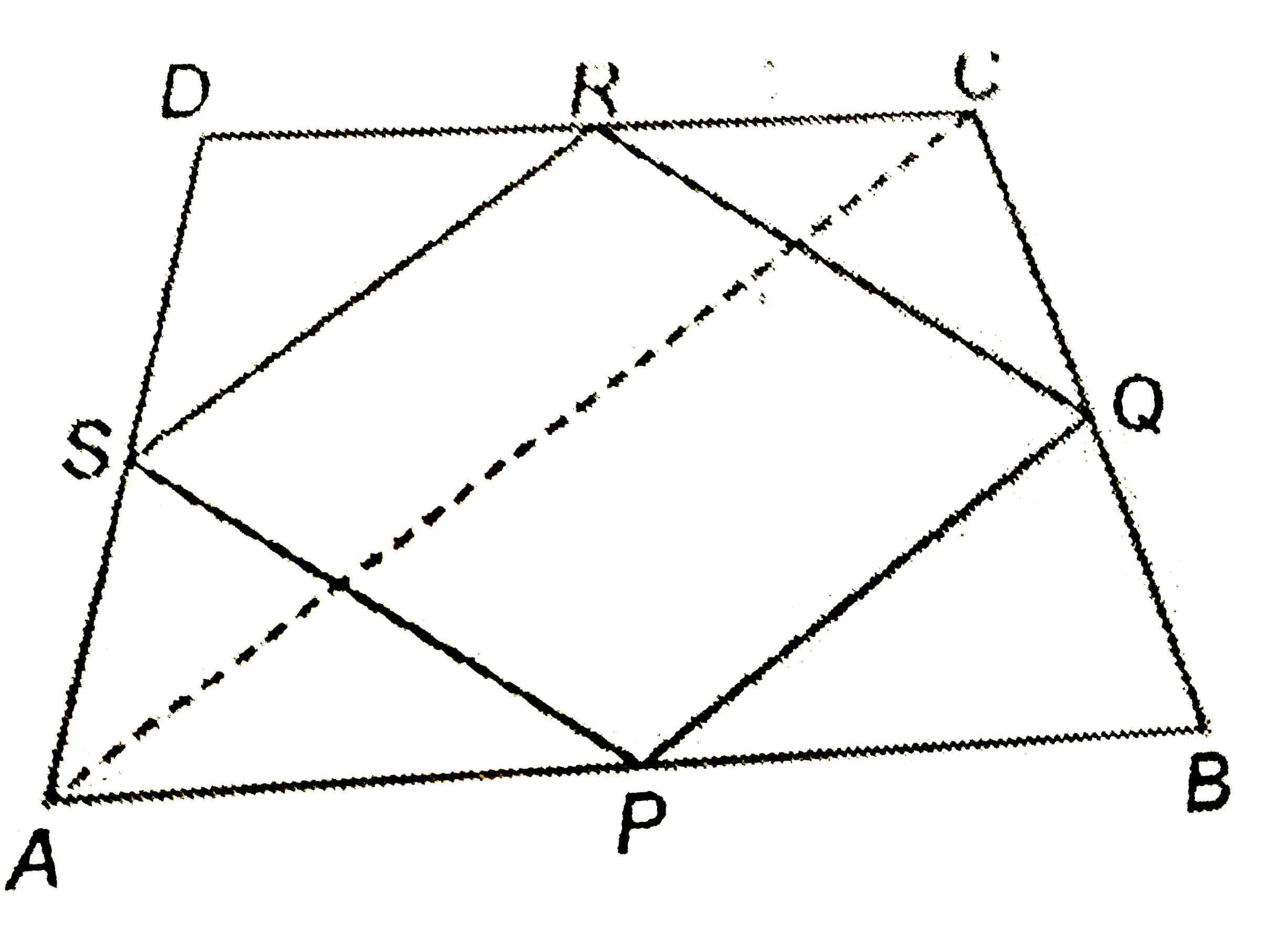
View SolutionProve that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View SolutionThe figure formed by joining the mid-point of the adjacent sides of a parallelogram is a rectangle (b) parallelogram (c) rhombus (d) square
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionWe get a rhombus by joining the mid-points of the sides of (a) parallelogram (b) rhombus (c) rectangle (d) triangle
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area. GIVEN : A parallelogram ABCD in which BD is one of the diagonals. TO PROVE : ar (ABD)=ar(CDB)
View SolutionProve that the line segments joints joining the mid-points of the adjacent sides of a quadrilateral from a parallelogram.
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View Solution