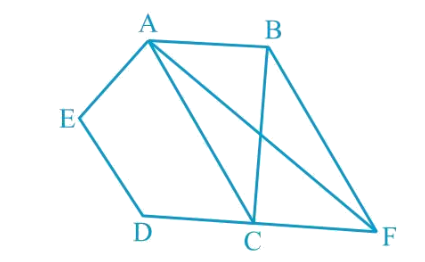
In Figure, ABCD is a quadrilateral and BE⊥AC and also BE meets DC produced at E , Show that area of ADE is equal to the area of the quadrilateral ABCD.

△ABCand△EAC
Are on same base AC and between same parallels
∴AC is parallel to BC
∴ar(△ABC)=ar(EAC)
⇒Adding ar(△ADC) to both sides
ar(△ABC)+ar(△ADC)=ar(△ECA)+ar(△ADC)
ar(QuadrilateralABCD)=ar(△ADE)
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a quadrilateral and BE∣AC and also BE meets DC produced at E. Show that area of ADE is equal to the area of the quadrilateral ABCD
 View Solution
View SolutionIn the given figure, compute the area of quadilateral
 View Solution
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
 View Solution
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionProve that the diagonals of quadrilateral ABCD,AC and BD intersect in O. Prove that if BO=OD, the triangles ABC and ADC are equal in area.
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
 View Solution
View Solution

