Question

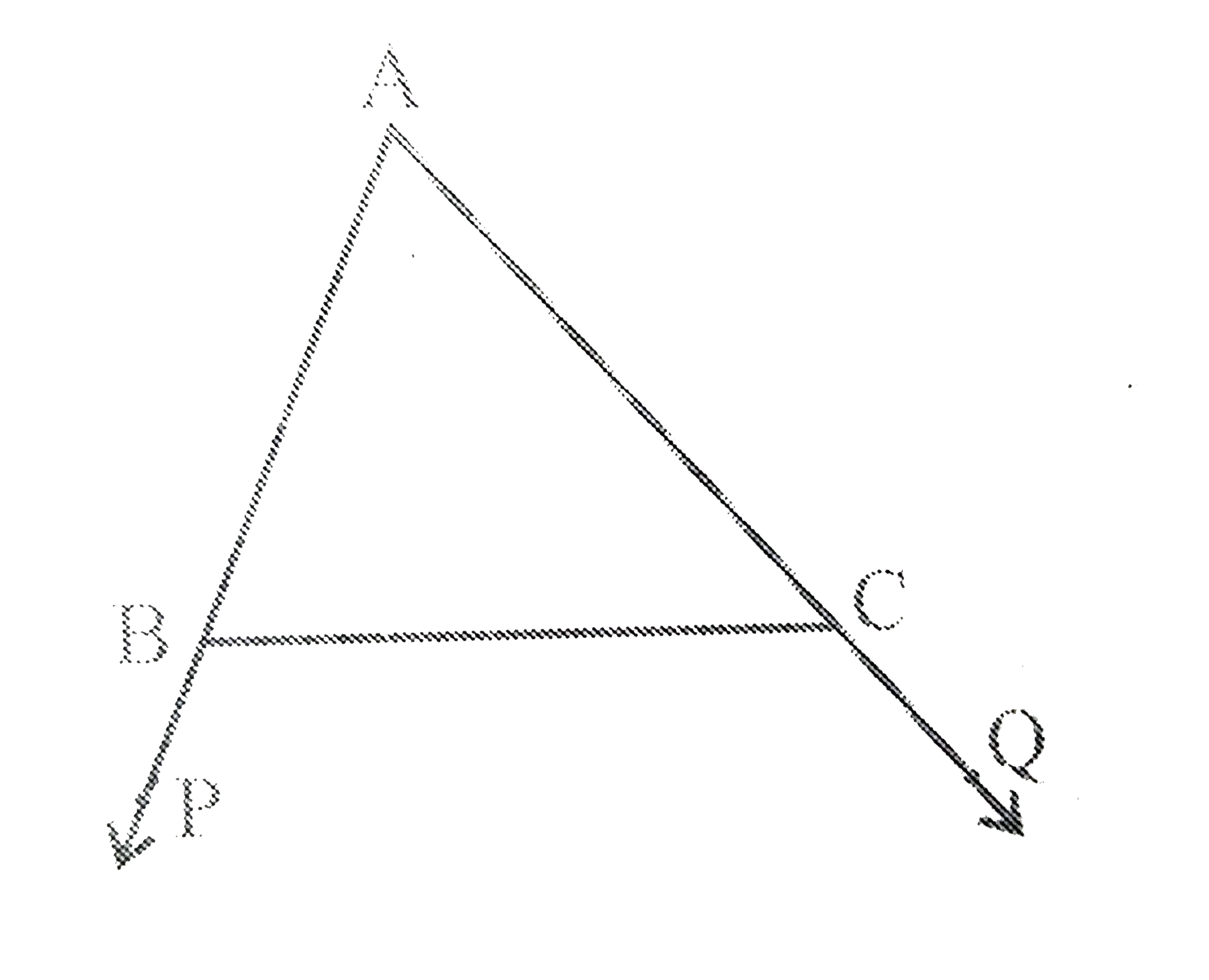
The sides $AB$
and $AC$
of a $ABC$
are produced to $P$
and $Q$
respectively. If the bisectors of $\angle PBC$
AND $\angle QCB$
intersect at $O,$
then
$\angle BOC={90}^0-\frac{1}{2}\angle A$
GIVEN : A $ABC$
in which sides $AB$
and $AC$
are produced to $P$
and $Q$
respectively. The bisectors of $\angle PBC$
and $\angle QCB$
intersect at $O\stackrel{.}{}$

Explanation

Given: Bisectors of angle `PBC` and angle `QCB` intersect at `O`.
To prove: `∠BOC=90^@- 1/2∠A`
Proof: `∠BAC=∠A`
Exterior angle`=`Sum of opposite interior angles
`∠PBC=∠C+∠A`
`∠QCB=∠B+∠A`
`∠CBO=(1/2)∠PBC=(1/2)(∠C+∠A)`
`∠BCO=(1/2)∠QCB=(1/2)(∠B+∠A)`
`∠CBO+∠BCO+∠BOC=180^@` (Sum of angles of a triangle)
`(1/2)(∠C+∠A)+(1/2)(∠B+∠A)+∠BOC=180^@`
`(1/2)(∠C+∠A +∠B)+(1/2)∠A+∠BOC=180^@`
`(1/2)180^@+1/2∠A+∠BOC=180^@`
`90^@+1/2∠A+∠BOC=180^@`
`∠BOC=90^2-1/2∠A`
Hence Proved