In a right angled triangle, one acute angle is double the other. Prove that the hypotenuse is double the smallest side. GIVEN : A ABC in which ∠B=900 and ∠ACB=2∠CAB . to prove : AC=2BC CONSTRUCTION : Produce CB to D such that BD=CB. Join AD.
Given: △ABC in which ∠B=90∘ and ∠ACB=2∠CAB.
To prove: AC=2BC
Construction: Produce CB to D such that BD=CB. Join AD
Proof : In △ABD and △ABC,
BD=BC [By construction]
AB=AB [Common]
∠ABD=∠ABC=90∘
By SAS criterion of congruence, we get:
△ABD≅△ABC
AD=AC and ∠DAB=∠CAB [By CPCT]
AD=AC and ∠DAB=x [∴∠CAB=x]
Now,
∠DAC=∠DAB+∠CAB=x+x=2x
∴∠DAC=∠ACD
DC=AD [Side Opposite to equal angles]
2BC=AD [since DC=2BC]
2BC=AC [AD=AC]
Hence, Hypotenuse is twice the smallest angle.
Topper's Solved these Questions
Similar Questions
In a right angled triangle with sides a and b and hypotenuse c , the altitude drawn on the hypotenuse is x . Prove that ab=cx .
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC , prove that BD=12AC . GIVEN : A ABC in which ∠B=900 and D is the mid-point of AC. TO PROVE : BD=12AC CONSTRUCTION Produce BD to E so that BD=DE. Join EC.
View SolutionThe sum of any two sides of a triangle is greater than the third side. GIVE : A ABC
View SolutionProve that any two sides of a triangle are together greater than twice the median drawn to the third side. GIVEN : ABC in which AD is a median. PROVE : AB+AC>2AD CONSTRUCTION : Produce AD to E such that AD=DE. Join EC.
View SolutionShow that the difference of any two sides of a triangle is less than the third side. GIVEN : ABC TO PROVE : (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC CONSTRUCTION : Take a point D on AC such that AD=AB. Join BD.
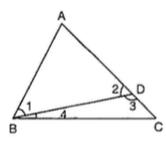
View SolutionIf two sides of a triangle are unequal, the longer side has greater angle opposite to it. GIVEN : A ABC in which AC>AB. TO PROVE : ∠ABC>∠ACB
CONSTRUCTION : Mark a point D on AC such that AB=AD. Joint BD.
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle. GIVEN : A ABC in which AD⊥BC,BE⊥AC and CF⊥AB. PROVE : AD+BE+CF<AB+BC+AC
View SolutionIn ΔABC, if angle C=3 angle A, B C=27 and A B=48 , then find the length of the side A C .
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn a right angle triangle with sides a,b,c, a circle is drawn inside is touching its sides to prove= a+b−c2=radius of circle.
View Solution