Show that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle. GIVEN : A in which and PROVE :
Let ABC be the triangle with sides BC, AC, AB opposite angles A, B, C being in length equal to a, b, c respectively.
Draw perpendiculars AD, BE and CF from A, B, C to opposite sides meeting sides BC, AC and AB at D, E, F respectively.
Now perpendicular -----(1)
Also, ------(2)
Likewise , ----(3)
Adding inequalities (1), (2), (3),
Topper's Solved these Questions
Similar Questions
Show that the difference of any two sides of a triangle is less than the third side. GIVEN : ABC TO PROVE : (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC CONSTRUCTION : Take a point D on AC such that AD=AB. Join BD.
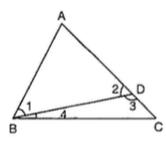
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : A ABC in which AD is the bisector of ∠A meeting BC in D such that BD=DC.
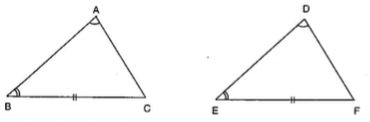
View SolutionTwo triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle. GIVE : Two sABC and DEF such that ∠B=∠E,∠C=∠F and BC=EF TO PROVE : ABC≅DEF
View Solution(a,b),(c,d),(e,f) are the vertices of an equilateral triangle.Then the orthocenter of the triangle is
View SolutionShow that the difference of any two sides of a triangle is less than the third side. Given : A ABC To Prove: (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC Construction: Take point D on AC such that AD=AB . Join BD
View SolutionProve that the sum of three altitudes drawn from the vertices to opposite sides of a triangle is less than the sum of three sides.
or
Prove that the perimeter of a triangle is greater than the sum of three altitudes drawn from the vertices to opposite of a triangle.
View SolutionIf any two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle, then the two triangles are congruent. GIVEN : Two sABC and DEF such that ∠A=∠D,∠B=∠E,BC=EF TO TROVE : ABC≅DEF
View SolutionThe sum of any two sides of a triangle is greater than the third side. GIVE : A ABC
View SolutionIn a right angled triangle, one acute angle is double the other. Prove that the hypotenuse is double the smallest side. GIVEN : A ABC in which ∠B=900 and ∠ACB=2∠CAB . to prove : AC=2BC CONSTRUCTION : Produce CB to D such that BD=CB. Join AD.
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.

View Solution