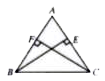
In given figure the altitudes AD, BE and CF , the altitudes of triangle ABC are equal. Prove that ABC is an equilateral triangle.
Video Solution
Text Solution
(each 90)
AD=BE(given)
(common)
-(1)
(each 90)
(given)
(common)
(AAS)
AB=CB-(2)
from equation 1 and 2
Hence, is equilateral.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then

∠DCB=A∠EBCB∠ECBC∠ABDD∠DBCIn the given figure, BD and CE are the altitudes of triangle ABC such that BD = CE, then

ΔCBD is congruent toAΔCBEBΔBCECΔBECDΔECB
AD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAngle A, B, C of a triangle ABC are equal to each other. Prove that ABC is equilateral.
View SolutionFind the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View SolutionABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that
AB=AC, i.e., ABC is an isosceles triangle.
View SolutionIf AD, BE, CF are the altitudes of triangle ABC whose ortho centre is H then C is ortho centre of
View SolutionIf AD, BE and CF are medians of triangle ABC then prove that median AD divides line segment EF.
View Solution
