A horizontal tube has different cross sections at points and . The areas of cross section are and respectively, and pressures at these points are and where is the density of liquid flowing in the tube and and are heights of liquid columns in vertical tubes connected at and . If , then the flow rate of the liquid in the horizontal tube is
The correct Answer is:A
Using Bernoulli’s concept
Hence, (Volumetric flow )
Similar Questions
A vertical U-tube has two liquids 1 and 2. The heights of liquids columns in both the limbs are h and 2h, as shown in the figure. If the density of the liquid 1 is 2ρ.
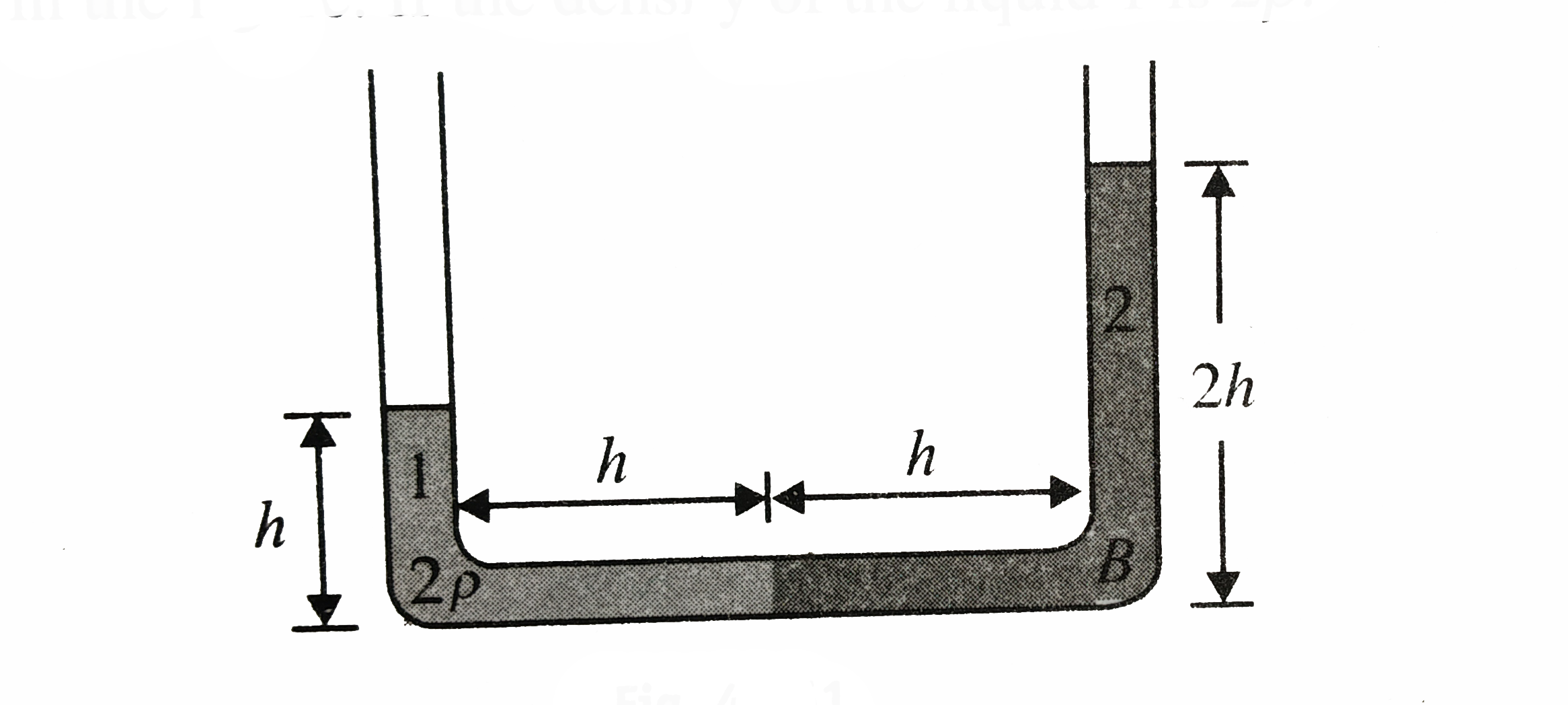
a. Find the density of liquid 2.
b. If we accelerate the tube towards right till the heights of liquid columns will be the same, find the acceleration of the tube.
View SolutionThe ratio of the radius of the tube of a venturimeter is η(η>1) . The ratio of the densities of the liquid in the manometer and the moving fluid is η1 . If the difference in heights of the liquid column in the manometer is h , find the minimum speed of flow of the fluid .
View Solution
Knowledge Check
The formula for height of a liquid column (h) in a capillary tube is
Ah=2TrpgBh=2TcosθrpgCh=2TsinθrpgDh=T2cosθrpgThe most approprite graph between height (h) of the liquid column in a capillary tube and the radius ( r ) of the tube for a given liquid will be
A B
B C
C D
D
From a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.
 AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section A1 and A2 and v1 and v2 respectively. The difference in the levels of the liquid in the two vertical tubes is h, then

View SolutionA liquid flows through a pipe of non-uniform cross-section. If A1andA2 are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
View SolutionA horizontal tube of non uniform cross section has radii fo 0.1 m and 0.05 m respectively at M and N,
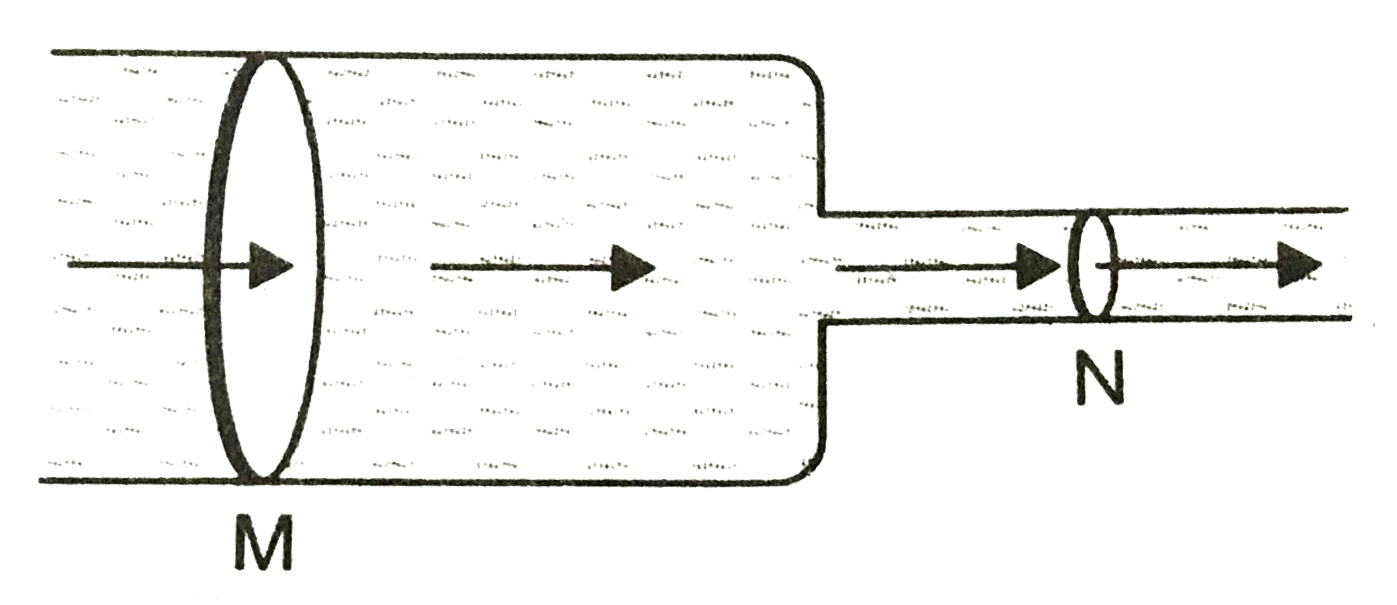
For a streamline flow of liquid the rate of liquid flow is
View SolutionIn a capillary tube having area of cross - section A, water rises to a height h. If cross-sectional area is reduced to A9, the rise of water in the capillary tube is
View SolutionA vertical U-tube contains a liquid of densityρ and surface tension T. if the radius of the meniscus of liquid in the limbs of the U-tube are R1 and R2 find the difference in the liquid column in the limbs.
View Solution