A liquid moves in a smoothh tube of uniform cross section. Find the pressure $P_{2}$ at point $2$ of the tube if the pressure at point $1$ of the extended tube is $P_{1}$ and the vertical distance between points $1$ and $2$ is $h$ . brgt

Video Solution

Text Solution

Verified by Experts

Since the cross section of the tube is uniform.
$A_{1} = A_{2} = A$
Then applying equation of continuity at points $1$ and $2$ , we have
$v_{1} = v_{2}$ ……i
Substuting $v_{1} = v_{2} (= v)$ in Bernoulli's equation we have
$P_{1} + \frac{1}{2} ρ v^{2} + ρ g h_{1} = P_{2} + \frac{1}{2} ρ v^{2} + ρ g h_{2}$
This gives $P_{1} + ρ g h_{1} + P_{2} + ρ g h_{2}$
Since $h_{1} - h_{2} = h$ , we have $P_{2} = P_{1} + ρ g h$

|

Updated on:21/07/2023

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Suppose the pressure at the surface of mercury in as barometer tube is $P_{1}$ and the pressure at the surface of mercury in the cup is $P_{2}$ .
A $P_{1} = 0, P_{2} =$ atgmospheric pressure
B $P_{1}$ = atmosphereic pressure $P_{2} = 0$
C $P_{1} = P_{2} =$ atmospheric pressure
D $P_{1} = P_{2} = 0$
Question 2 - Select One
A tube of uniform cross section is used to siphon water from a vessel $V$ as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure $(P_{0})$ . The height of the tube above and below the water level in the vessel are $h_{1}$ and $h_{2}$ , respectively.

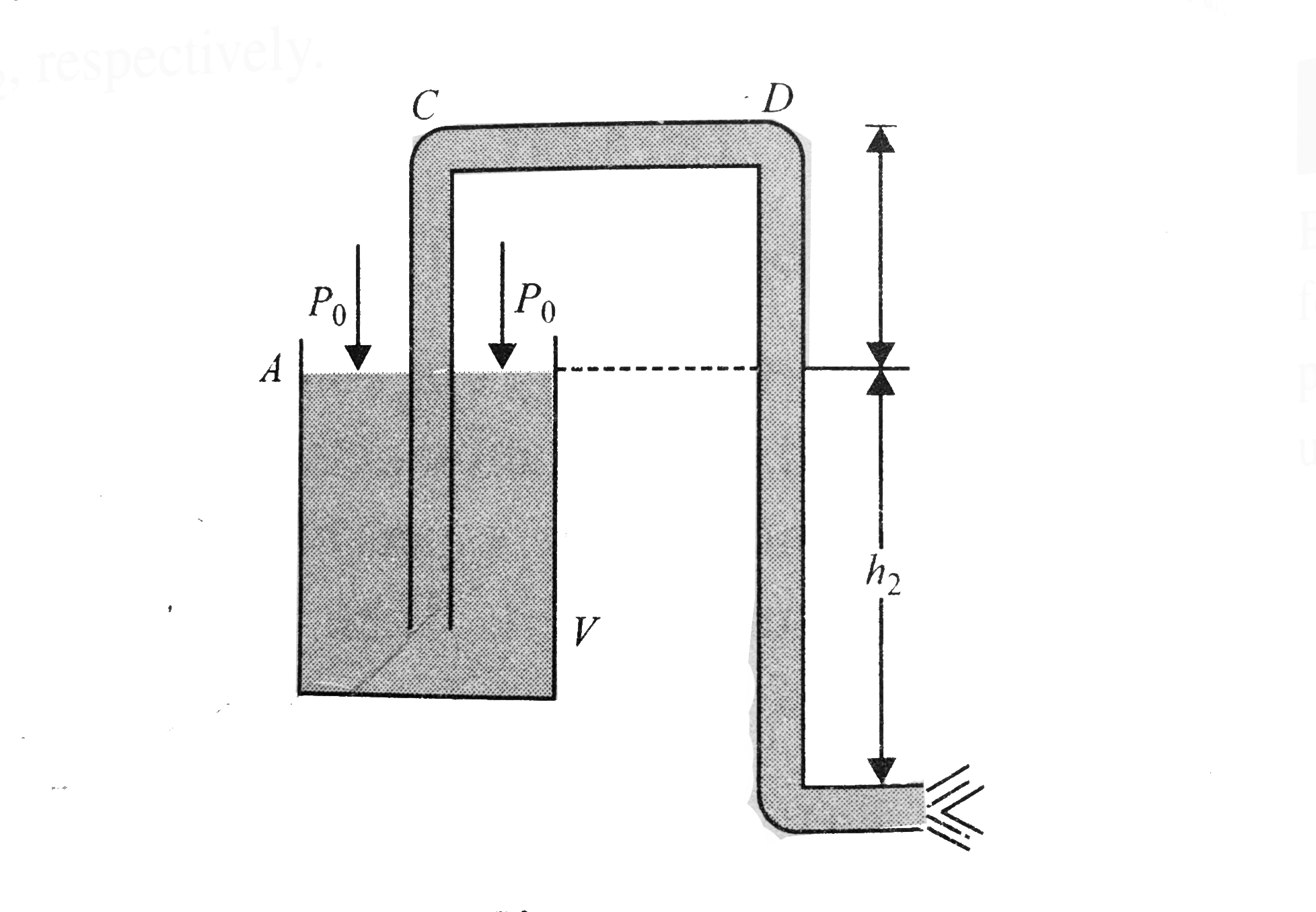
Given $h_{1} = h_{2} = 3.0 m$ , the gauge pressure of water in the highest level $C D$ of the tube will be
A $3.0 \times 10^{4} N / m^{2}$
B $5.9 \times 10^{4} N / m^{2}$
C $5.9 \times 10^{4} N / m^{2}$
D $1.5 \times 10^{4} N / m^{2}$
Question 3 - Select One
A tube of uniform cross section is used to siphon water from a vessel $V$ as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure $(P_{0})$ . The height of the tube above and below the water level in the vessel are $h_{1}$ and $h_{2}$ , respectively.

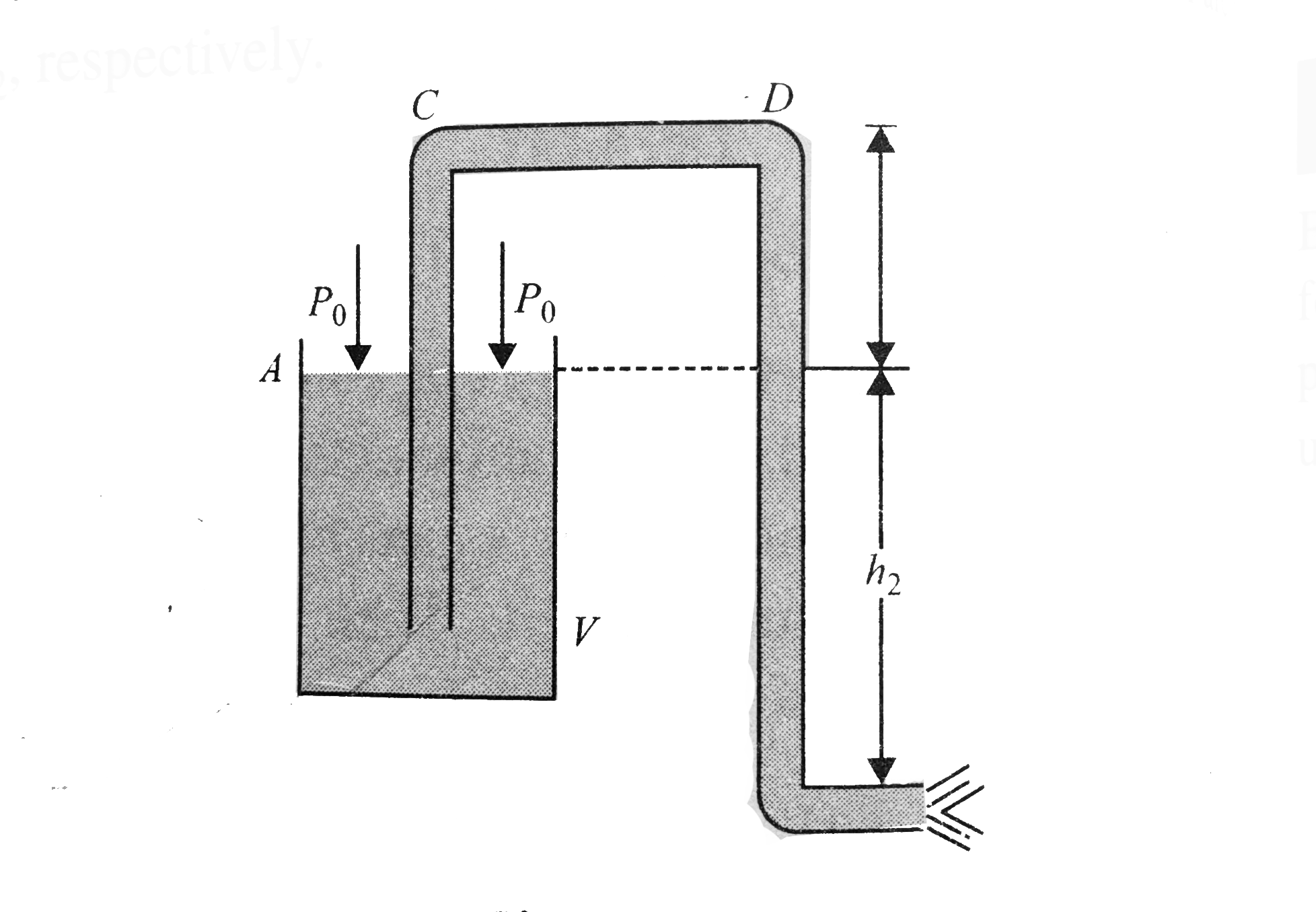
If $h_{1} = h_{2} = 3.0 m$ , the maximum value of $h_{1}$ , for which the siphon will work will be
A $3.0 m$
B $6.0 m$
C $7.2 m$
D $4.8 m$

CENGAGE PHYSICS-FLUID MECHANICS-INTEGER_TYPE

Home
Ask Doubt
Profile