A portion of a tube is shown in the figure. Fluid is flowing from cross-section area A1 to A2. The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A2 is √gl2. If the pressures at A1 & A2 are same, then the angle made by the tube with the horizontal will be:
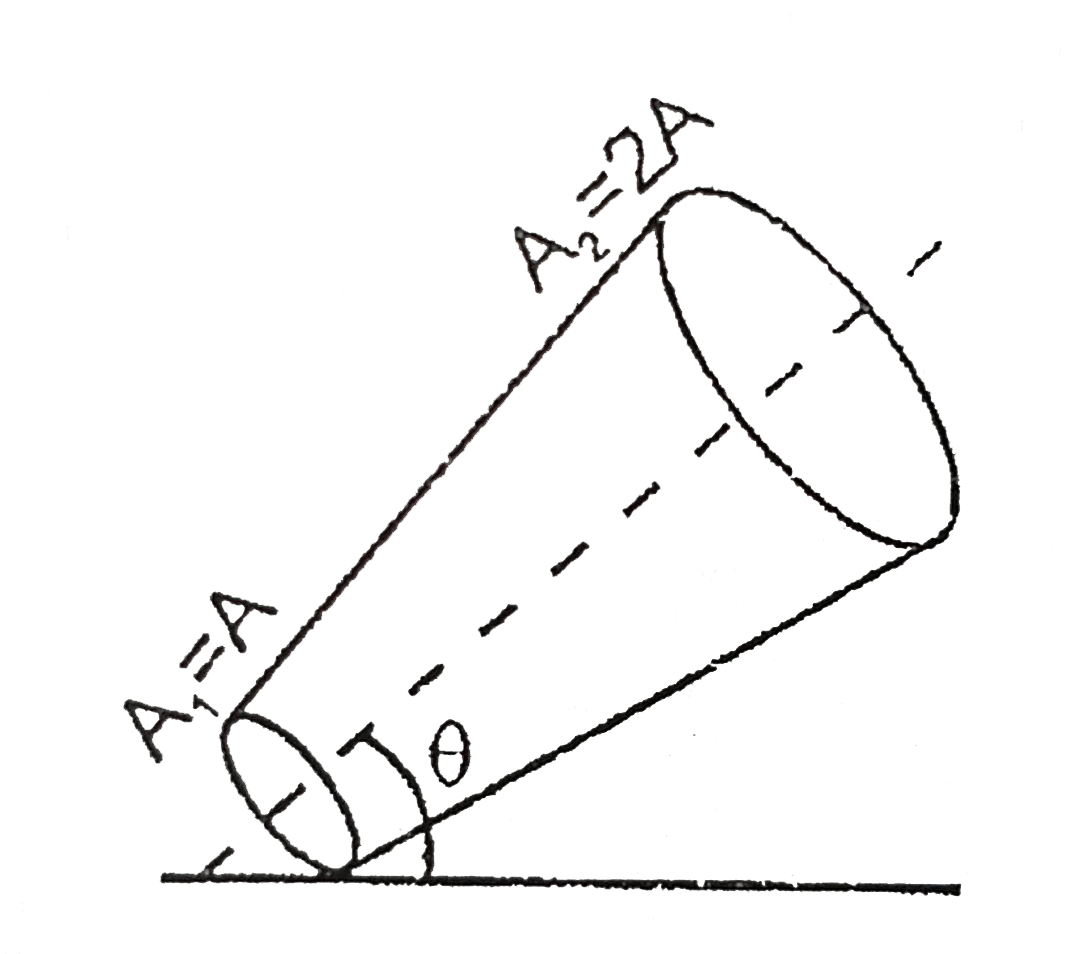
37∘C
sin−1'34
53∘C
cos−1'34
The correct Answer is:B
Step by step video, text & image solution for A portion of a tube is shown in the figure. Fluid is flowing from cross-section area A_(1) to A_(2). The two cross-sections are at distance 'l' from each other. The velocity of the fluid at section A_(2) is sqrt((gl)/(2)). If the pressures at A_(1) & A_(2) are same, then the angle made by the tube with the horizontal will be: by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - II
9 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - III
8 Videos
- FLUID MECHANICSBOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 1 PART - II Section (C)
6 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise
52 Videos
- FULL TEST 1BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise
30 Videos
Similar Questions
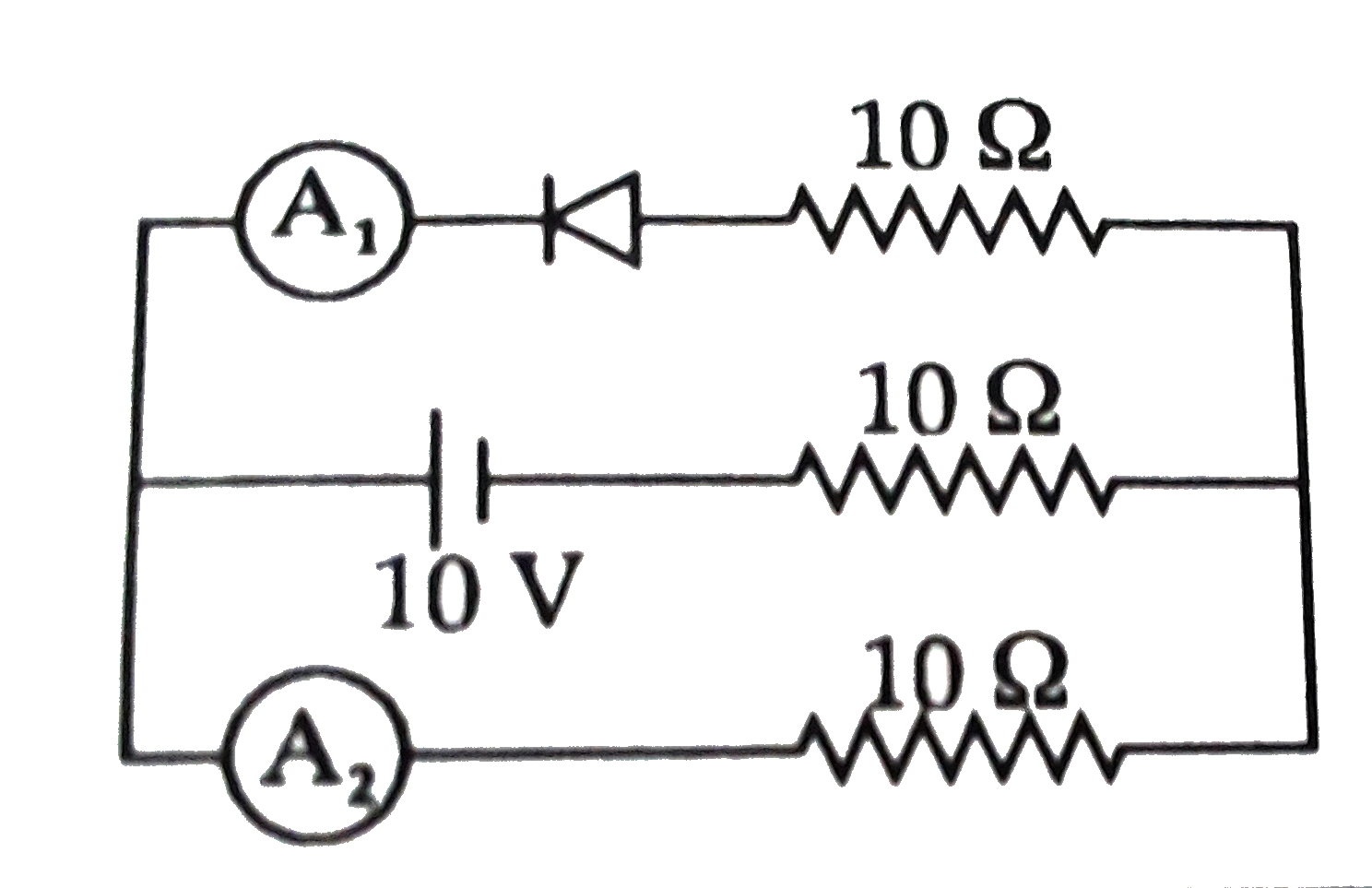
In the figure shown the readings of the ammeters A1andA2 are respectively.
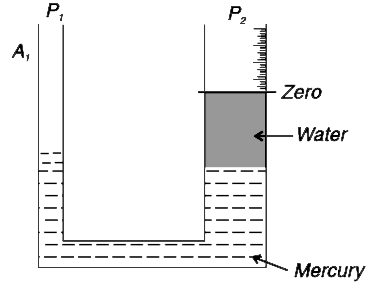
View SolutionA monometer has mercuty and water filled in it as shown in the figure A scale is marked on the right tube which has a cross sectional area of A2. The other tube has a cross sectional area of A1. When pressures P1 and P2 at both ends of the manometer is same, the level of water in the right side is at the zero of the scale. When the applied pressure P1 is changed by ΔP0, the level of water surface changes by Δh. the quantity ΔhΔP0 can be defined as pressure sensitivity(s) of the manometer. Calculate the pressure sensitivity of the given manometer. Density of water and mercury is ρω and ρHg respectively.
View Solution
Knowledge Check
A liquid flows through a pipe of non-uniform cross-section. If A1andA2 are the cross-sectional areas of the pipe at two points, the ratio of velocities of the liquid at these points will be
AA1A2BA1A2CA2A1D1A1A2From a horizontal tube with area of cross-section A1 and A2 as shosn in fiugre liquid is flowing in the level of the liauid in the two veritcal tunes is h.
 AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tube
AThe volume of the liquid flowing through the tube in time is A1v1Bv2−v1=√2ghCv22−v11=2ghDThe energy per unit mass of the liquid is the same in both sections of the tubeThree batteries are connected as shown in figure. Reading of ideal ammeters A1,A2 & A3 are :
 A13A,0,13AB0.5A,0.5A & 1 A respectivelyCzero, 0.5A & zero respectivelyDzero, zero & 1A respectively
A13A,0,13AB0.5A,0.5A & 1 A respectivelyCzero, 0.5A & zero respectivelyDzero, zero & 1A respectively
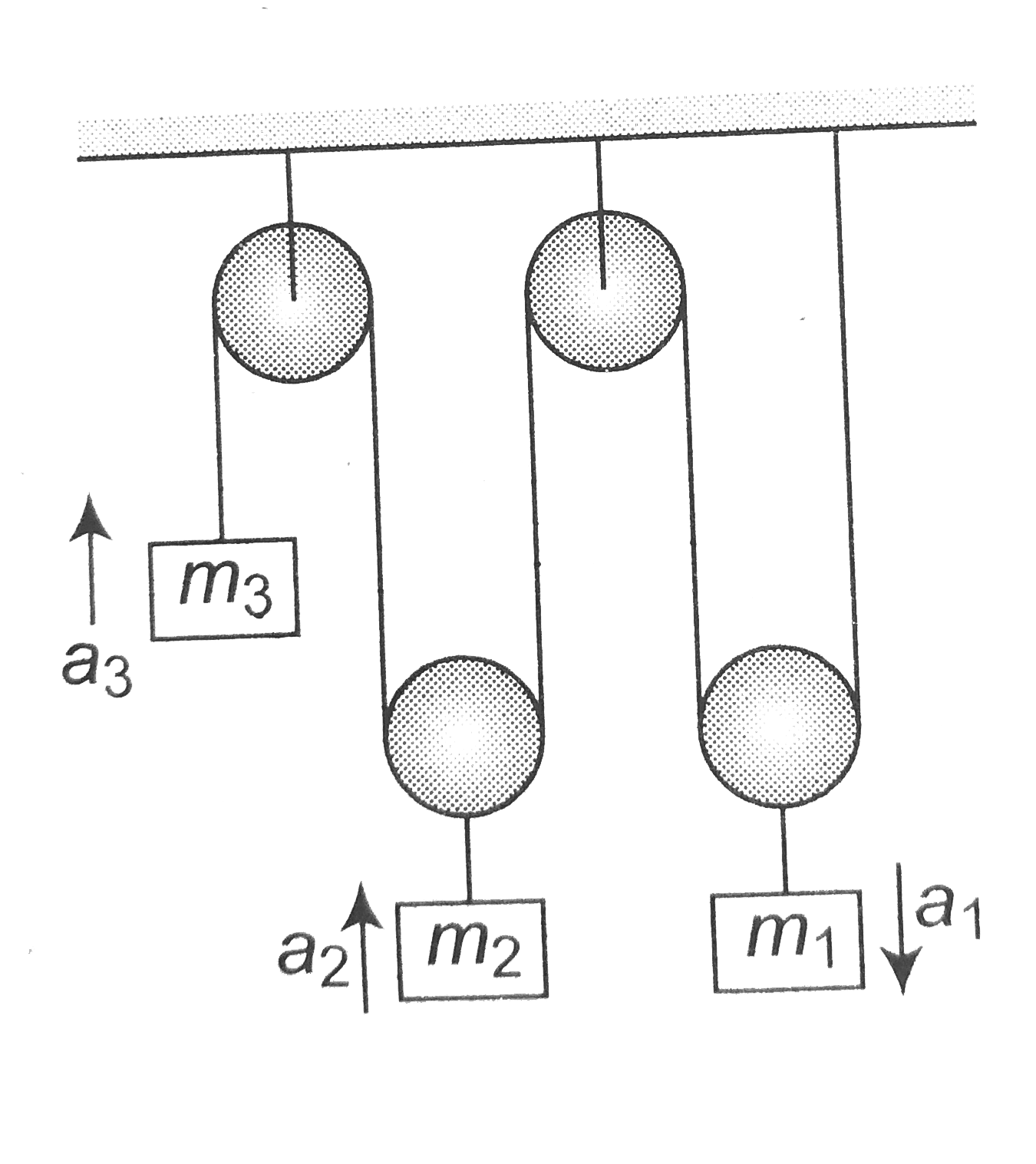
If the blocks are moving as shown in the figure the relation between a1 , a2 and a3 will be.
View SolutionTwo vectors →A1and→A2 each of magnitude A are inclinded to each other such that their resultant is equal to √3A. What is the magnitude of the resultant of →A1and−→A2 is
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
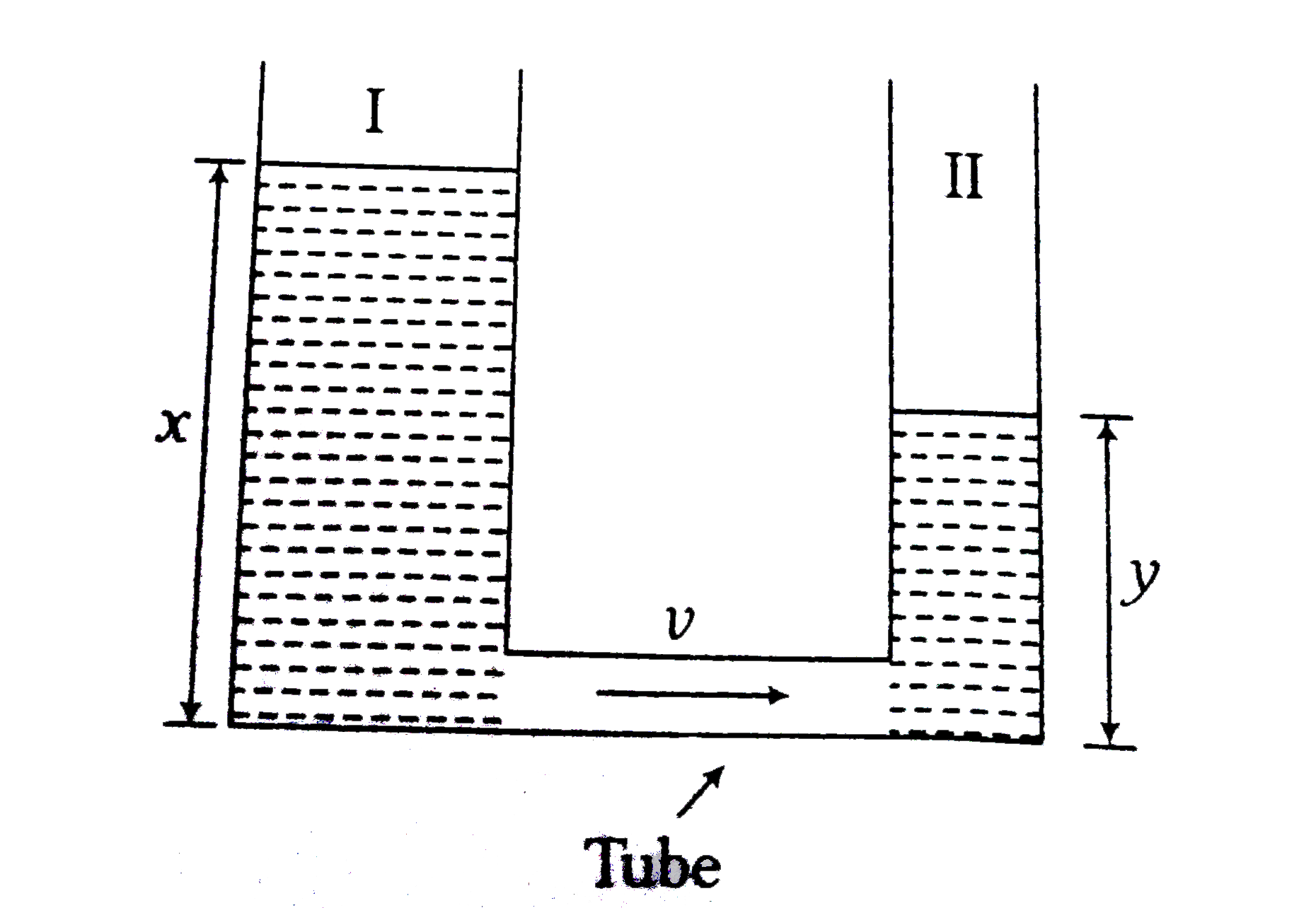
View SolutionA liquid flows in a tube from left to right as shown in figure. A1 and A2 are the cross-section of the portions of the tube as shown. Then the ratio of speeds v1/v2 will be

View SolutionA liquid flows in a tube from left to right as shown in figure. A1 and A2 are the cross-section of the portions of the tube as shown. Then the ratio of speeds v1/v2 will be

View Solution
