A ring is kept on a rough inclined surface. But the coefficient of friction is less than the minimum value required for pure rolling. At any instant of time let KTandKR be the translational and rotational kinetic energies of the ring, then
KR=KT
KR>KT
KT>KR
KR=0
The correct Answer is:C
Friction in this case is backward. If it is insufficient, it is a case of forward slipping or KT>KR.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises25videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.315videos
ROTATION
- BOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.15videos
RAY OPTICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
A block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
. View SolutionTwo blocks of masses m1andm2 are kept touching each other on a rough fixed inclined plane of inclination α. Coefficients of kinetic friction between the inclined plane and the block m1 is k1 and between the inclined plane and block m2 is k2. Find the force of interaction between the blocks in the process of motion.
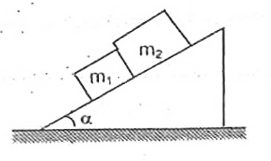
View Solution
Knowledge Check
- Question 1 - Select One
A flywheel rolls down on an inclined plane. At any instant of time, the ratio of rotational kinetic energy to total kinetic energy is :-
A1:2B3:1C4:3D1:3 - Question 2 - Select One
A block of mass ''m' is attached with a mass - less spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=3/4. The minimum value of 'M' required so that the block on the inclined plane is at rest (neglect mass of string and pulley).
A5m4B9m20C7m20D3m5 - Question 3 - Select One
A block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
A35mB45mC65mD32m
A block of mass 5 kg is kept on a rough horizontal surface. The coefficient of friction for the contact force block and surface are μs=0⋅1andμk=0⋅9 respectively . A horizontal force F given by F 0⋅5t is applied at t = 0 . Here t represent time in seconds . Determine the force of friction and acceleration of the block at
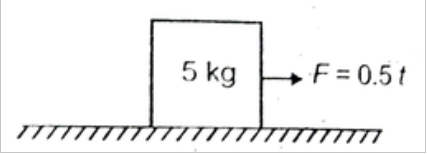
(i) t = 1s (ii) t= 10 s (iii) t = 12 sView SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a linear speed v0 in forward direction and an angular with a linear speed v0 in forward direction and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
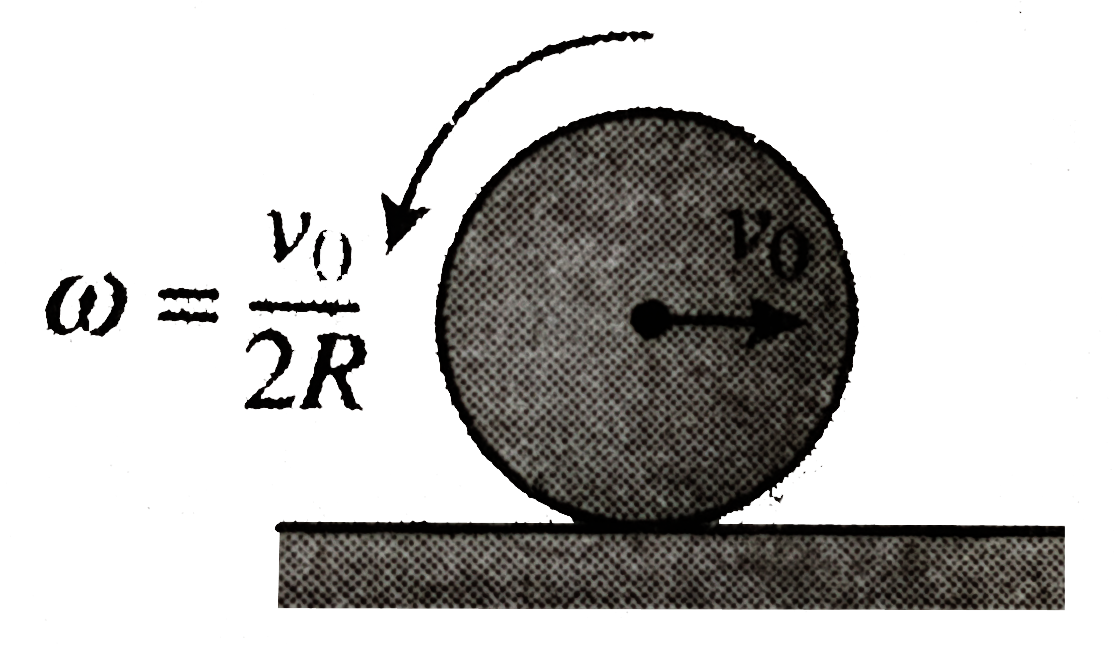
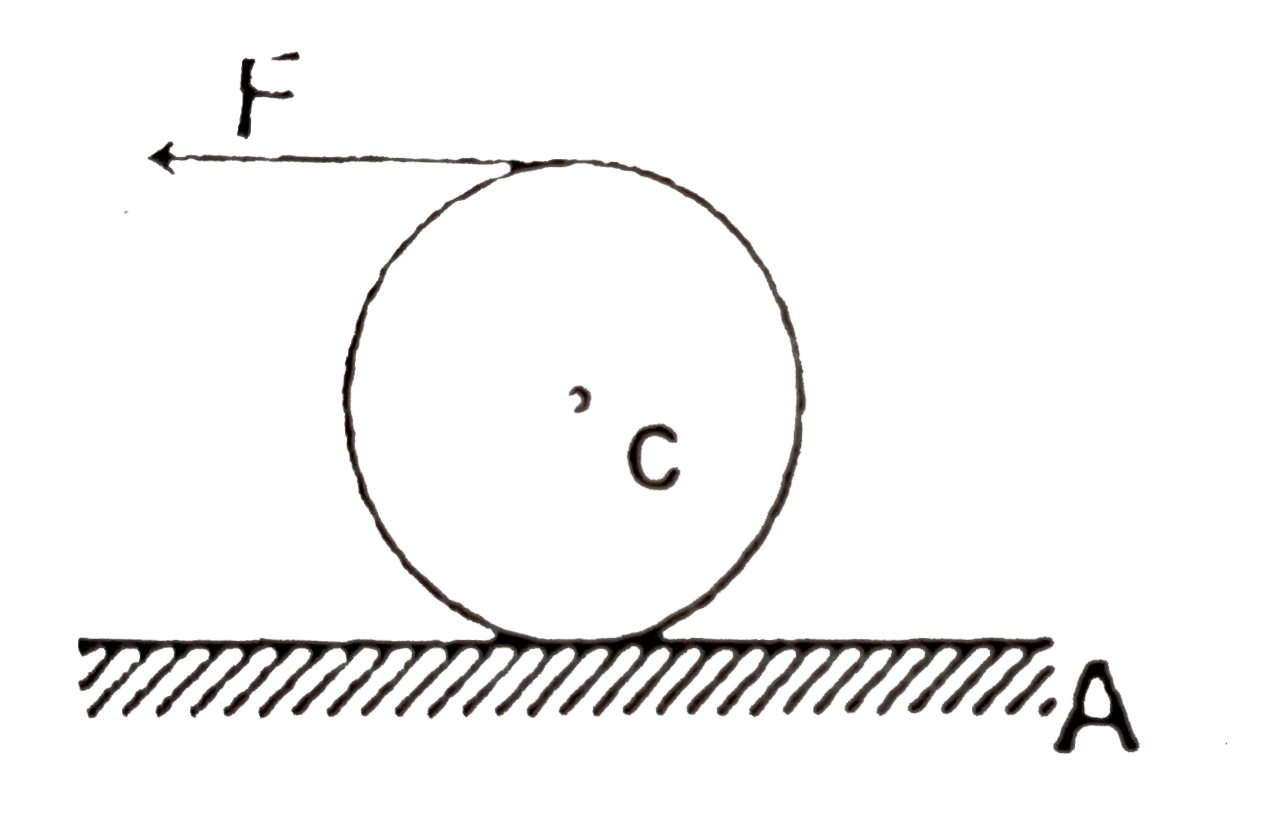
View SolutionA massless string is wrapped around a hollow cylinder having mass m and radius r. The cylinder is kept on a rough horizontal surface (coefficient of friction is μ). A constant force F is applied as shown in the figure. In case of pure rolling, the friction force acting on the bottom most point of the cylinder is
View SolutionA partical is realeased from the top of two inclined rought surface of height h each. The angle of inclination of the two planes are 30∘ and 60∘ respectively. All other factors (e.g. coefficient of friction , mass of the block etc) are same in both the cases. Let K1andK2 be the kinetic energy of the partical at the bottom of the plane in two cases. Then
View SolutionThe coefficient of friction between a particle moving with some velocity V0 and the rough horizontal surface is (V02gt0). Find how much kinetic energy is lost in time t0 due to friction :
View Solution