The coefficient of friction between a particle moving with some velocity V0 and the rough horizontal surface is (V02gt0). Find how much kinetic energy is lost in time t0 due to friction :
1/4
1/2
3/4
2/3
The correct Answer is:C
v1=v0−(μg)t0
=v0−(v02gt0)gt0=v0/2 ltMbrgt velocity left =v0/2
K.E left =12m(v02)2=14(12mv20)
=14 of initial K.E.
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Multiple Answer)
Explore 11 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Comprehension)
Explore 20 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Integer)
Explore 5 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
A block of mass m moving with a velocity v0 on a rough horizontal surface from x=0 coefficient of friction is given by μ=μ0=ax. Find the kinetic energy of the block as function of x before it comes to rest.
View SolutionIf a charged particle is projected on a rough horizontal surface with speed v0. Find the value of dynamic coefficient of friction, if the kinetic energy of system is constant.

View Solution
Knowledge Check
The coefficient of friction between two surface is 0.2. The maximum angle of friction is
Asin−1(0.2)Bcos−1(0.2)Ctan−1(0.1)Dcot−1(5)A small block of mass m is plced over a long plank of mass M the coefficient of friction between then is μ ground is smooth At t=0 m is given a velocity v1 and M a velocity v2(>v1) as shown in figure After this M is maintained at constant celeration a(<μg)
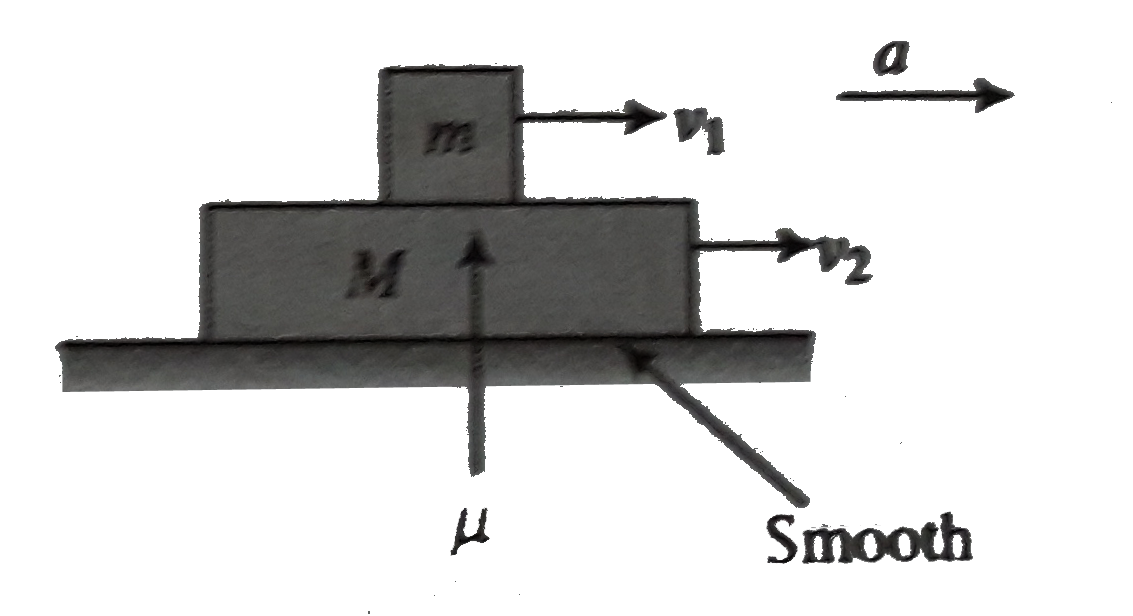
Initially there will be some relative motion between the block and the plank ,but after some time relative motion will cease and velocities of both will become
Find the forward force acting on the plank before after t0 respectively.AMa,(M+m)aBμmg+Ma,(M+m)aCμMg+ma+MaD(M+m)a,μmg+MaA particle moves with an intial velocity v0 and retardation αv, where v is its velocity at any time t.
AThe particle will cover a total distance v0/αBThe particle will come to rest after a time 1/αCThe particle will continue to move for a very long timeDThe velocity of the particle will become v0/2 after a time 1/α
A small body of mass m moving with velocity v0 on rough horizontal surface, finally stops due to friction. Find, the mean power developed by the friction force during the motion of the body, if the frictional coefficient μ=0.27,m=1 kg and v0=1.5ms−1.
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
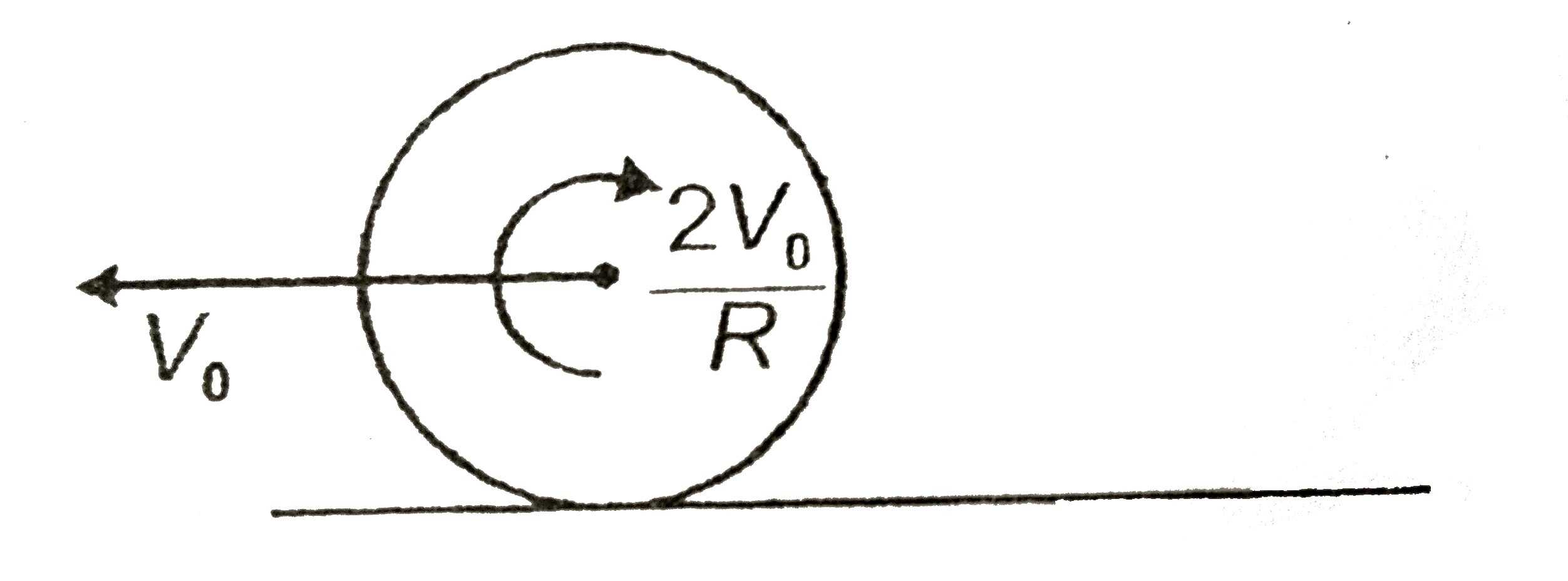
View SolutionA heavy box of mass 20 kg is pulled on a horizontal force.If the coefficient of kinetic friction between the box and the horizontal surface is 0.25, find the force of friction exerted by horizontal surface on the box.
View SolutionA particle moves with an initial velocity v0 and retardation αv, where v is the velocity at any time t.
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View Solution

