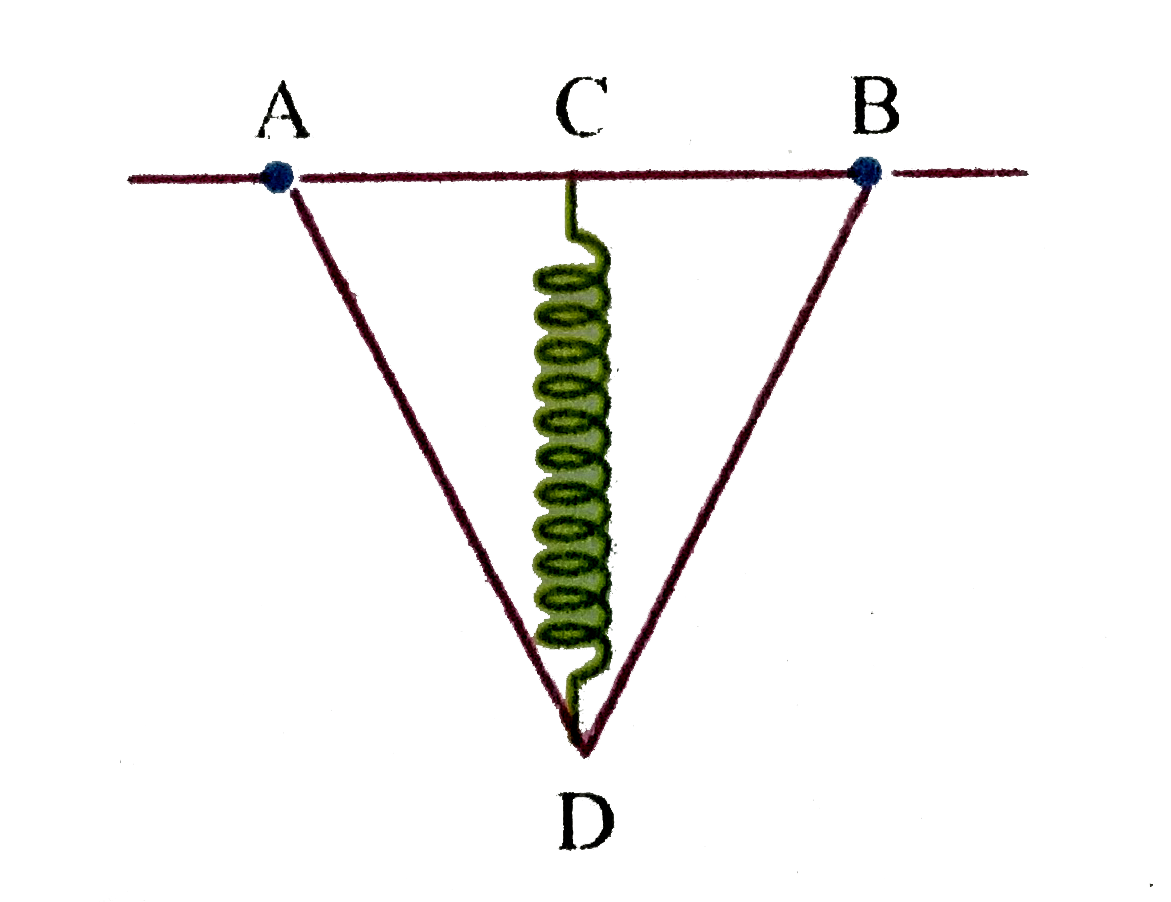
A and B are smooth light hinges equidistant from C, which can slides on ABC. The spring of force constant K is fixed at its one end C and conncented to light rods AD and BD at point D. A block of mass m is suspended at D. Find the velocity of the block, when ∠CAD changes from 30∘ to 45∘.AD=BD=L.
 .
.
[gL−KL22m(√2−1)2]12
[gL√2−KL22m(√2−1)2]12
[gL(√2−1)−KL24m(√2−1)2]12
[gL−KL22m]12
The correct Answer is:C
Initially, CD=Lsin30∘=L2
Finally, CD=Lsin45∘=L√2
Increase in elastic PE = Increase
in PE = Decrease in PE
12K(L√2−L2)2+12mv2=mg(L√2−L2)
On solving, v=[gL(√2−1)−KL24m(√2−1)2]12.
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Multiple Answer)
Explore 11 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Comprehension)
Explore 20 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Integer)
Explore 5 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
Two blocks A and B of equal mass m=1.0kg are lying on a smooth horizontal surface as shown in figure. A spring of force constant k=200N/m is fixed at one end of block A. Block B collides with block A with velocity v0=2.0m/s. Find the maximum compression of the spring.

View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View Solution
Knowledge Check
A spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv)Rod AO3 of length L can rotate abput A. Initially rod was at position AO2, when spring OB of force constant K, attached to block B of mass m was at position OA with unstretched length L. The smooth block B can slide on rod when pulled by the block D of mass m through a massless spring and smooth pulley at O1.
Find the velocity of the block B, when the rod and spring at B make an angle of 30∘ with their respective initial positions : (B is the middle point of the block)
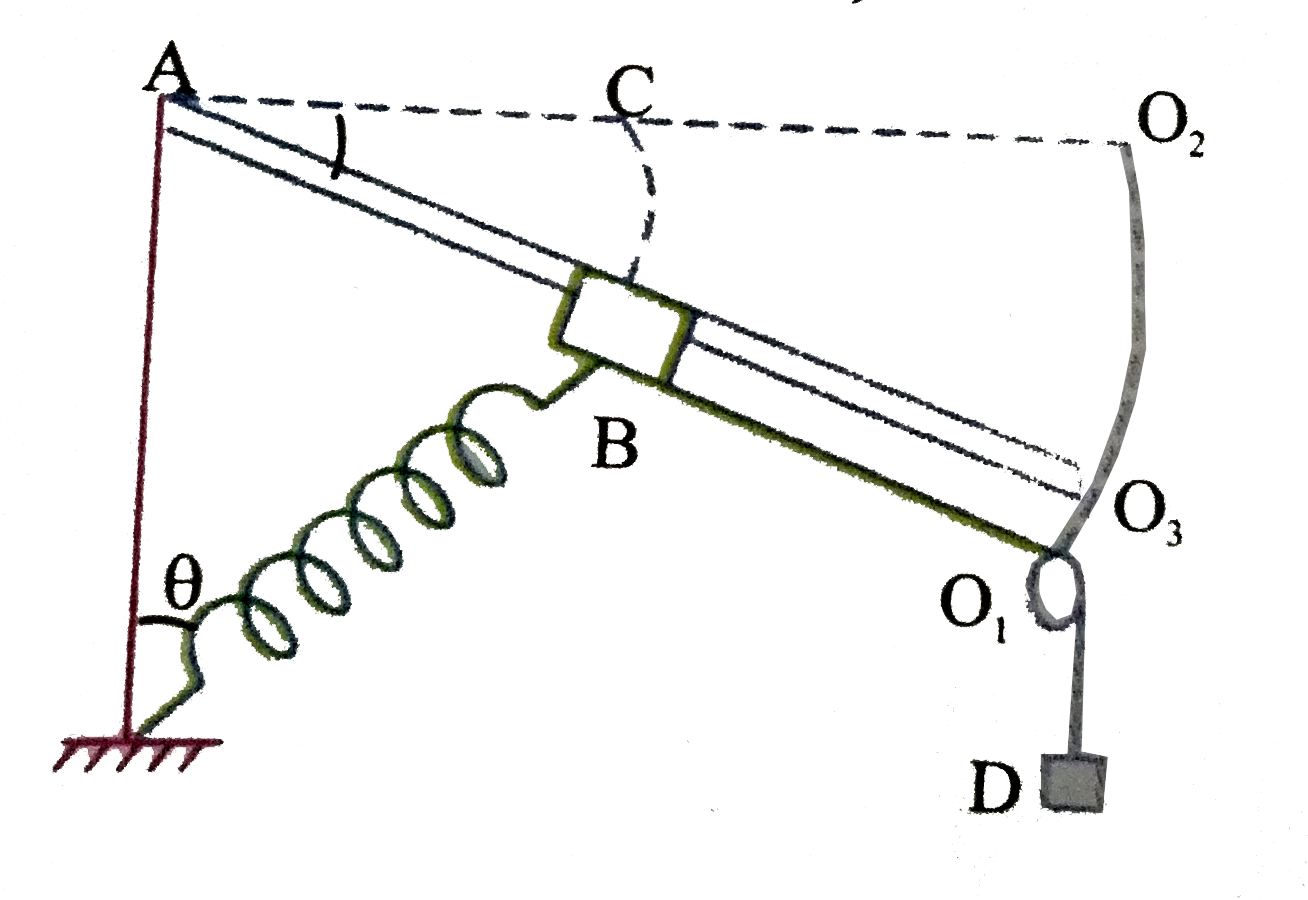 .A⎡⎢ ⎢ ⎢⎣10mgL−KL2(2−√3)28m⎤⎥ ⎥ ⎥⎦12B⎡⎢ ⎢⎣2mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12C⎡⎢ ⎢⎣5mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12D⎡⎢ ⎢⎣6mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12
.A⎡⎢ ⎢ ⎢⎣10mgL−KL2(2−√3)28m⎤⎥ ⎥ ⎥⎦12B⎡⎢ ⎢⎣2mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12C⎡⎢ ⎢⎣5mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12D⎡⎢ ⎢⎣6mgL−KL2(√2−1)4m⎤⎥ ⎥⎦12An ideal spring having force constant k is suspended from the rigid support and a block of mass M is attached to its lowe end. The mass is released from the natural length of the spring. Then the maximum exiension in the spring is
A4mgkB2MgkCMgkDMg2k
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
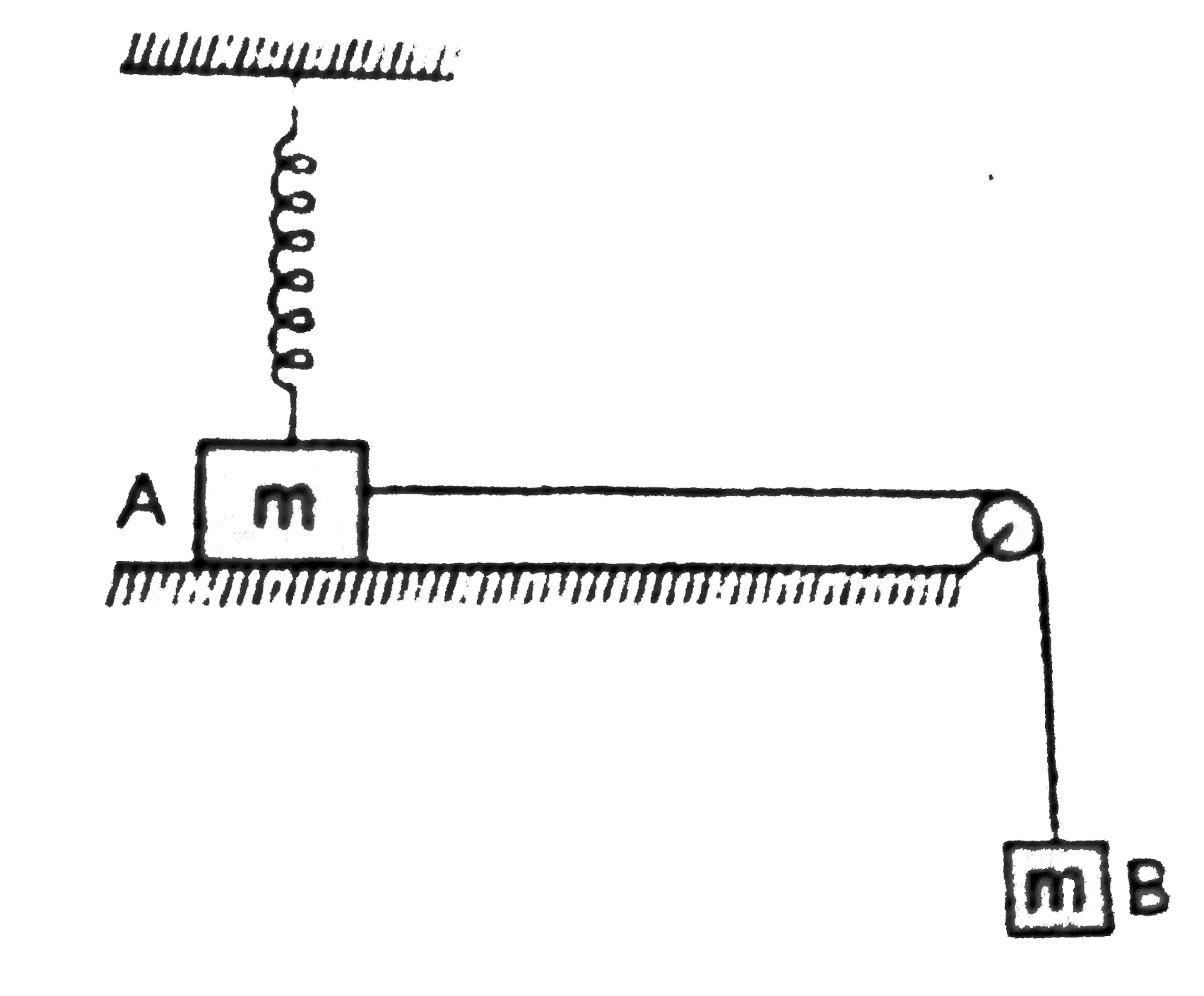
View SolutionFigure shows tow blocks A and B, each having a mass of 320 g connected by a light string passing over a smooth light puley. The horizontal surface on which the block A can slide is smooth. The blcok A is attached to a spring of lconstant 40 N/m whose other end is fixed to a support 40 cm the horizontal surface. Initially, the sprng is vertical and unstretched when the system is released to move. Find the velocity of theh block A at teh instnt it breaks of the surface below it. Take g=10ms2.
View SolutionTwo block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionOne end of a light spring constant k and natural length l0 is fixed and the other end is attached to a block of mass m lying on smooth horizontal surface. If the block is rotating in the horizontal circle of radius l, find the frequency of the revolution.
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
View Solution

