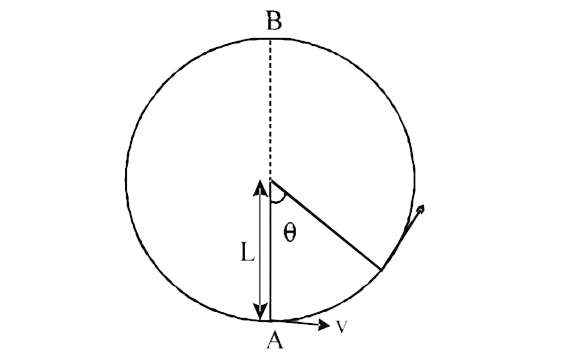
A bob of mass M is suspended by a massless string of length L. The horizonta velocity v at position A is just sufficient to make it reach the point B. The angle θ at which the speed of the bob is half of that at A, satisfies
θ=π4
π4<θ<π2
π2<θ<3π4
3π4<θ<π
The correct Answer is:D
As the body just reaches the topmost point B,
therefore, υA=√5gL and υB=√gL
Let at point Phaving angular displacement θ the speed becomes half of the initial value
υA. Using the law of conservation of energy
Energy at A = Energy at B
12mυ2A=12mυ2P+mgL(1−cosθ)
12m(υ2A−υ2P)=mgL(1−cosθ)
12m(5gL−5gL4)=mgL(1−cosθ)
158=(1−cosθ),cosθ=−78
Which means 3π4<θ<π.
Related Playlists
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Multiple Answer)11videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-VI (Comprehension)20videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Integer)5videos
WORK POWER AND ENERGY
- BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV43videos
WORK , ENERGY & POWER
Knowledge Check
- Question 1 - Select One
A mass m is hanging by a string of length l. The velocity v0 which must be imparted to it to just reach the top is
A√3glB√4glC√5glD√6gl - Question 1 - Select One
A bob of mass 10 M is suspended through an inextensible string of length I. When the bob is at rest at the equilibrium position, two particles of mass m each moving with velocity u making an angle 60° with the string strike and get simultaneously attached to the bob. What is the value of impulsive tension (Jtension) be string during the impact?
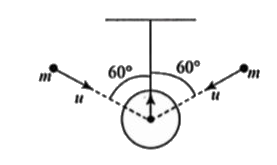 AZeroB2 muCmuD12 mu
AZeroB2 muCmuD12 mu - Question 1 - Select One
The bob of a simple prendulum is suspended by a strinng of length 80 cm . What minimum horizontal velocity should be imparted to the bob so that it reaches it reaches the height of suspension point ? (g=10m/s2)
A3m/sB4m/sC2m/sD5m/s - Question 1 - Select One
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elasticallywith another bob of mass 2m suspended by a string of length l2, which is initially at rest. Both strings are massless and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l2/l1 is (5/4)n. The value of n is
A3B6C9D5
Similar Questions
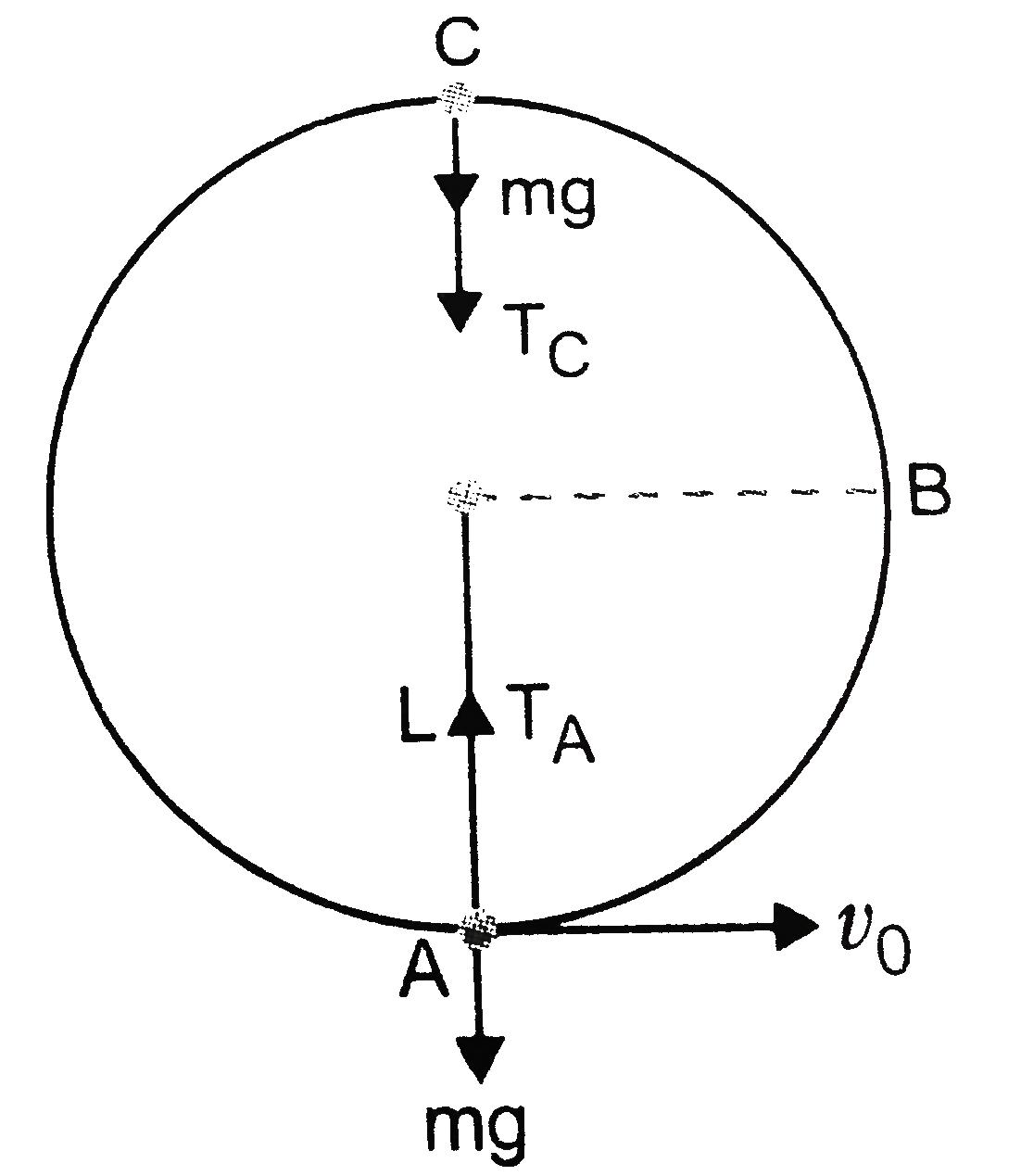
A bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity v0 at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack on reaching the topmost point C, figure, Obtain an expression for (i) v0 (ii) the speeds at points B and C, (ii) the ration of kinetic energies (KB/KC) at B and C.
Comment on the nature of the trajectory of the bob after it reahes the poing C.
 View Solution
View SolutionA bob of mass m is suspended by a light inextensible string of length l from a fixed point such that it is free to rotate in a vertical plane. The bob is given' a speed of √4gl horizontally. The, height of the bob from the lower most point where the string just becomes slacked is nl3. Find n.
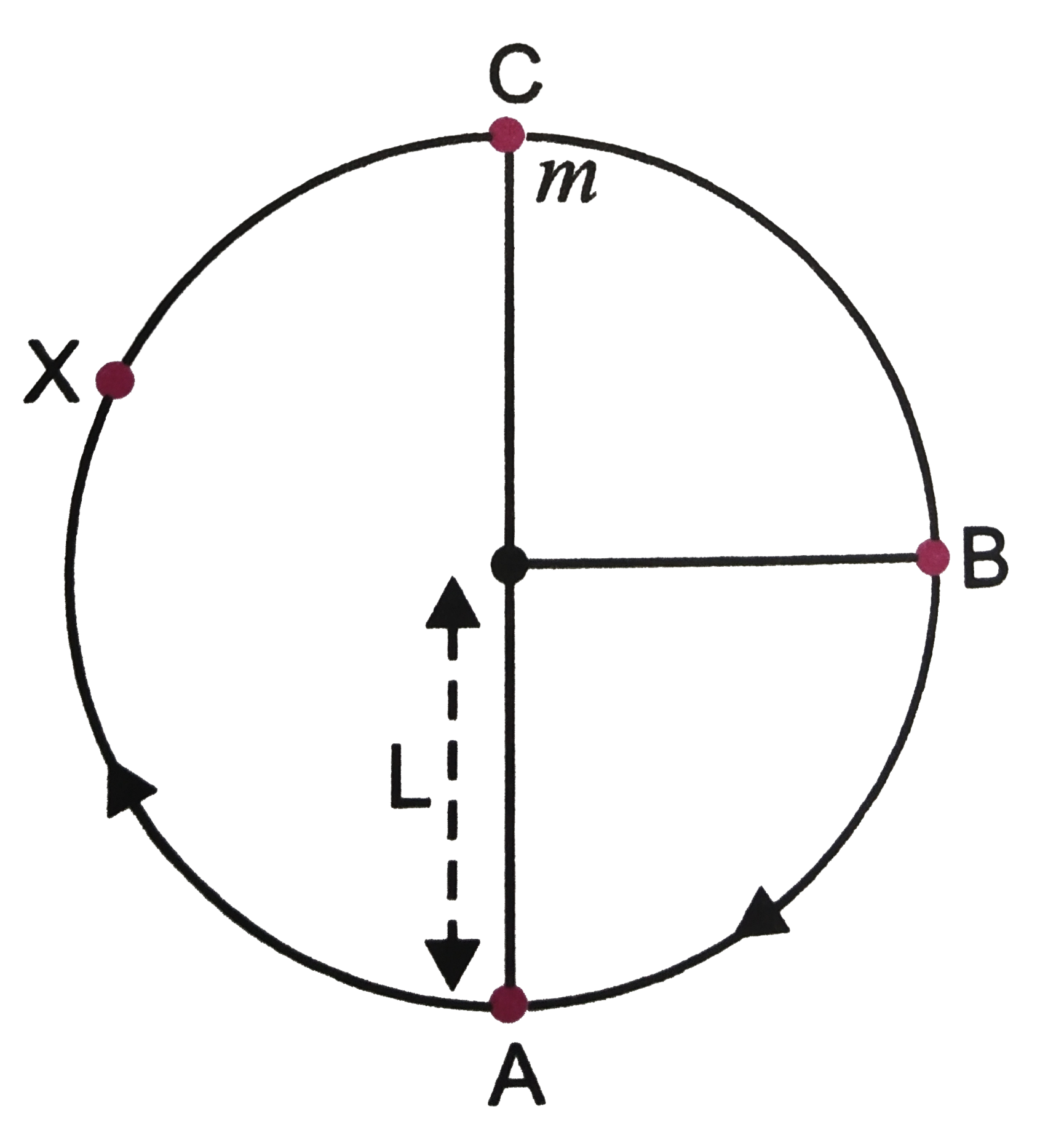
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure . What will be the trajectory of the particle if the string is cut at
(a) Point B ? (b) Point C? (c) Point X?
 View Solution
View SolutionA bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in figure. What will be X the trajectory of the particle if the string is cut at
(a) Point B
(b) Point C
(c) Point X
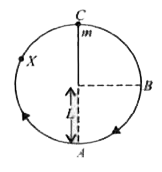 View Solution
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2View SolutionA bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio l1l2 is
View Solution

