A particle moves move on the rough horizontal ground with some initial velocity V0. If 34 of its kinetic enegry lost due to friction in time t0. The coefficient of friction between the particle and the ground is.
V02gt0
V04gt0
3V04gt0
V0gt0
The correct Answer is:A
To solve the problem step by step, we need to analyze the given information about the particle's motion and the energy lost due to friction.
Step 1: Understand the Initial Conditions
The particle has an initial velocity V0 and it loses 34 of its kinetic energy due to friction in time t0.
Step 2: Calculate Initial Kinetic Energy
The initial kinetic energy (KE_initial) of the particle can be calculated using the formula:
KEinitial=12mV20
Step 3: Determine Final Kinetic Energy
Since the particle loses 34 of its kinetic energy, the final kinetic energy (KE_final) will be:
KEfinal=KEinitial−34KEinitial=14KEinitial=14(12mV20)=18mV20
Step 4: Relate Final Kinetic Energy to Final Velocity
The final kinetic energy can also be expressed in terms of the final velocity Vf:
KEfinal=12mV2f
Setting the two expressions for KEfinal equal gives:
18mV20=12mV2f
Cancelling m from both sides and solving for Vf:
18V20=12V2f⟹V2f=14V20⟹Vf=V02
Step 5: Apply the Equation of Motion
Using the first equation of motion:
Vf=V0−at0
Where a is the retarding acceleration due to friction. The retarding force due to friction is given by:
Ffriction=μmg
Thus, the acceleration a is:
a=Ffrictionm=μg
Substituting this into the equation of motion gives:
V02=V0−μgt0
Step 6: Rearranging the Equation
Rearranging the equation to solve for μ:
μgt0=V0−V02=V02
μ=V02gt0
Final Answer
The coefficient of friction μ between the particle and the ground is:
μ=V02gt0
The particle has an initial velocity V0 and it loses 34 of its kinetic energy due to friction in time t0.
The initial kinetic energy (KE_initial) of the particle can be calculated using the formula:
KEinitial=12mV20
Since the particle loses 34 of its kinetic energy, the final kinetic energy (KE_final) will be:
KEfinal=KEinitial−34KEinitial=14KEinitial=14(12mV20)=18mV20
The final kinetic energy can also be expressed in terms of the final velocity Vf:
KEfinal=12mV2f
Setting the two expressions for KEfinal equal gives:
18mV20=12mV2f
Cancelling m from both sides and solving for Vf:
18V20=12V2f⟹V2f=14V20⟹Vf=V02
Using the first equation of motion:
Vf=V0−at0
Where a is the retarding acceleration due to friction. The retarding force due to friction is given by:
Ffriction=μmg
Thus, the acceleration a is:
a=Ffrictionm=μg
Substituting this into the equation of motion gives:
V02=V0−μgt0
Rearranging the equation to solve for μ:
μgt0=V0−V02=V02
μ=V02gt0
The coefficient of friction μ between the particle and the ground is:
μ=V02gt0
Topper's Solved these Questions
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Multiple Answer)
Explore 11 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-VI (Comprehension)
Explore 20 Videos
- WORK POWER AND ENERGYBook:NARAYNAChapter:WORK POWER AND ENERGYExercise:Level-V (Integer)
Explore 5 Videos
- WORK , ENERGY & POWER Book:NARAYNAChapter:WORK , ENERGY & POWER Exercise:EXERCISE IV
Explore 43 Videos
Similar Questions
A block begins to move on a rough horizontal surface with an initial velocity u. If it loses of its initial kinetic energy in time t, the coefficient of kinetic friction between the block and the surface is
View SolutionA body moving on the ground with a velocity of 15m/s comes to rest after covering a distance of 25m If acceleration due to gravity is 10m/s2 Calculate the coefficient of friction between the ground and the body .
View Solution
Knowledge Check
A particle moves on a rough horizontal ground with some initial velocity say ν0. If (3/4)th of its kinetic energy is lost in friction in time t0, then coefficient of friction between the particle and the ground is:
Aν02gt0Bν04gt0C3ν04gt0Dν0gt0A aprtical moves on a rough horizontal ground with same initial velocity say v0. If (3/4)th of its kinetic energy is lost in friction in time t0 , then coefficient of friction between the partical and the ground is:
Av02gl0Bv04gl0C3v04gl0Dv0gl0A particle is projected directly along a rough plane of inclination θ with velocity u. If after coming to the rest the particle returns to the starting point with velocity v, the coefficient of friction between the partice and the plane is
Au2v2tanθBu2−v2u2+v2tanθCv2u2tanθDu2+v2u2−v2tanθ
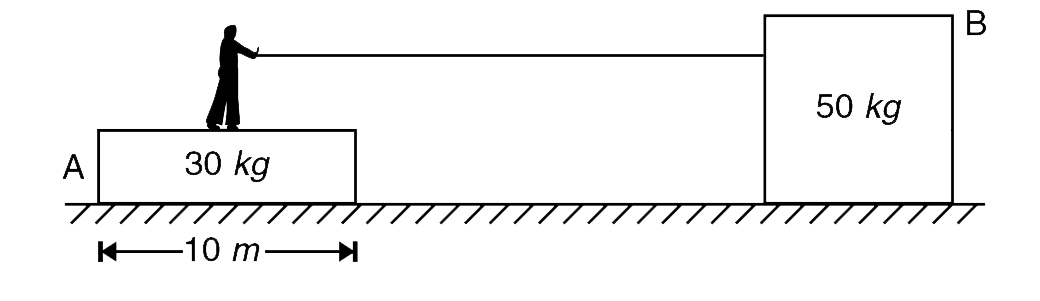
A 50 kg man is standing at the centre of a 30 kg platform A. Length of the platform is 10 m and coefficient of friction between the platform and the horizontal ground is 0.2. Man is holding one end of a light rope which is connected to a 50 kg box B. The coefficient of friction between the box and the ground is 0.5. The man pulls the rope so as to slowly move the box and ensuring that he himself does not move relative to the ground. If the shoes of the man does not slip on the platform, calculate how much time it will take for the man to fall off the platform. Assume that rope remains horizontal, and coefficient of friction between shoes and the platform is 0.6.
View SolutionA block starts moving up an inclined plane of inclination 30∘ with an initial velocity of v0 . It comes back to its initial position with velocity v02 . The value of the coefficient of kinetic friction between the block and the inclined plane is close to I1000 , The nearest integer to I is ____________ .
View SolutionA positively charged particle of mass m and charge q is projected on a rough horizontal x-y plane surface with z-axis in the vertically upward direction. Both electric and magnetic fields are acting in the region and given by →E=−E0ˆkand→B=−B0ˆk , respectively. The particle enters into the field at (a0,0,0) with velocity →v=v0ˆj. The particle starts moving in some curved path on the plane. If the coefficient of friction between the particle and the plane is μ. Then calculate the
(a) time when the particle will come to rest
(b) distance travelled by the particle when it comes to rest.

View SolutionA uniform ring of mass 'm' and radius 'R' is projected horizontally with velcoty v0 on a rough horizontal floor, so that it starts off with a purely sliding motion and it acquires a pure rolling motion after moving a distance d. If the coefficient of friction between the ground and ring is μ, then work done by the friction in the process is
View SolutionThe air of density ρ and moving with a velocity v strikes perpendicular the inclined surface of area A and of a wedge kept on a horizontal surface. The mass of the wedge is m. Assuming the collisions to be perfectly inelastic, the minimum value of the coefficient of friction between the wedge and the ground so that the wedge does not move is (Assume mass of particles of air is negligible)

View Solution

