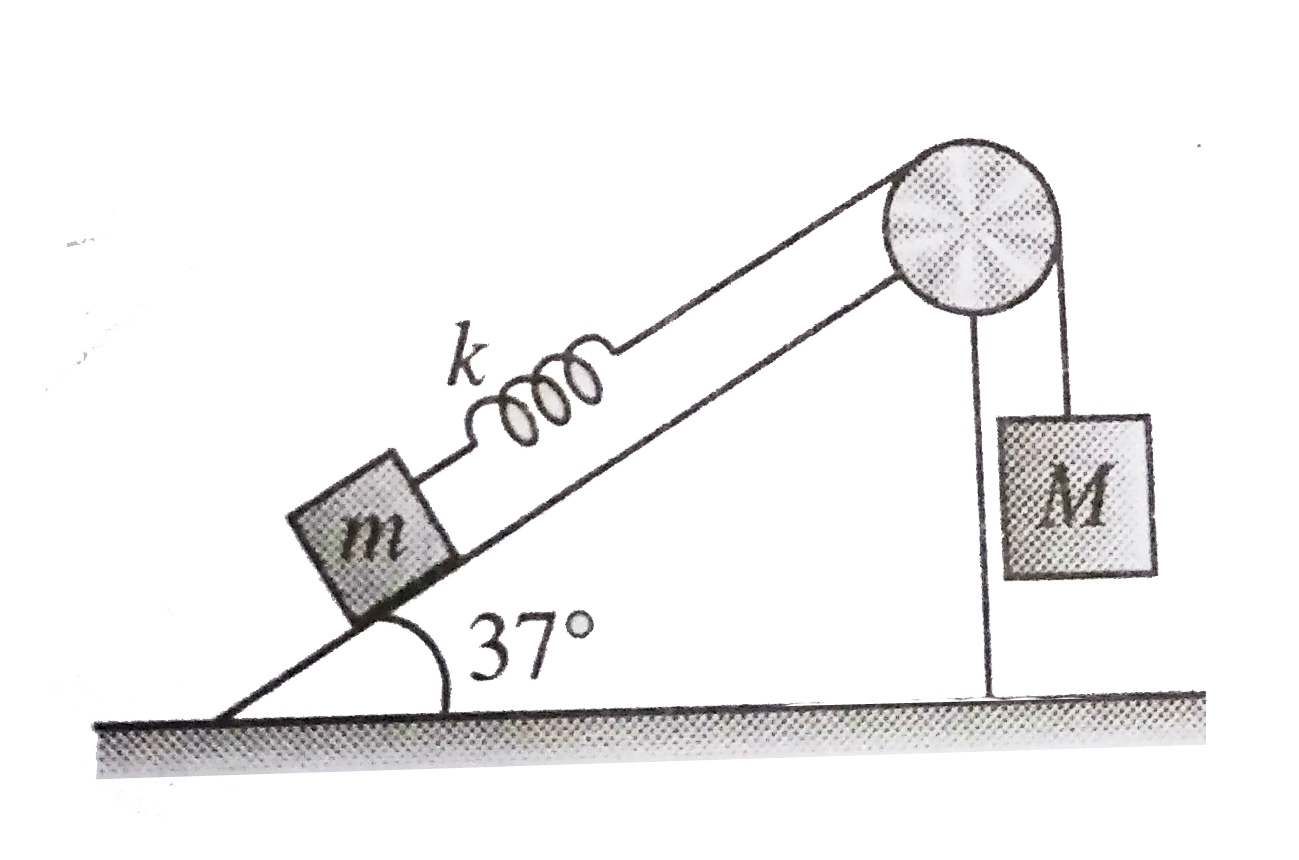
A block of mass m is attached with a massless spring of force constant K. the block is placed over a rough inclined surface for which the coefficient of friction is μ=34 find the minimum value of M required to move the block up the place. (Neglect mass of string and pulley. Ignore friction in pulley).
 .
.
The correct Answer is:C
Let Xm is maximum extension of spring. Then decrease in potential energy of M= increase in elastic potential energy of spring<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/DCP_V01_C09_E01_095_S01.pngwh=80%mx-autosty≤=background:white;>.<br>:. 1/2kX_(m)^(2) =MgX_(m)<br>orX_(m) =(2Mg)/(k)<br>Now,kX_(m) =mg sin 37^@ + mumg cos 37^@<br>or2Mg = (mg) (3/5) +(3/4)mg(4/5)<br>:. M =3/5m.
Similar Questions
Two blocks, each of mass m are attached with a massless and inextensible string. One of the blocks is placed on the rough horizontal surface of a table for which coefficient of friction μ. Find out the force exerted by the table on the block if μ>1.

View SolutionA block of mass m attached with a an ideal spring of force constant k is placed on a rough inclined plane having inclination θ with the horizontal and coefficient of friction μ=1/2tanθ, Initially the block is held stationary with the spring in its relaxed state, find the maximum extension in the spring if the block is released.

View Solution
Knowledge Check
A block of mass m is attached with a massless spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=34. The minimum value of M required to move the block up the plane is (Neglect mass of string, mass of pulley and friction in pulley)
 A35mB45mC65mD32m
A35mB45mC65mD32mA block of mass ''m' is attached with a mass - less spring of force constant k. The block is placed over a rough inclined surface for which the coefficient of friction is μ=3/4. The minimum value of 'M' required so that the block on the inclined plane is at rest (neglect mass of string and pulley).
 A5m4B9m20C7m20D3m5
A5m4B9m20C7m20D3m5A block of mass m attached with a massless spring of force constant k The block is placed over a rought inclined surface for which the coefficient of friction is 0.5M is released from rest when the spring was unstretched The minimum to move the value of M required to move the block m up the plane is (neglect mass of spring and pulley and friction in pulley)
 Am/2Bm/3Cm/4DNone of these
Am/2Bm/3Cm/4DNone of these
A block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass m is attached with a massless spring of force constant k. The block is placed over a fixed rought inclined surface for which the coefficient of friction is μ=34 . The block of mass m is initially at rest . The block is mass M is released from rest with spring in unstretched state. The minimum value of M required to move the block up the plane is ( neglect mass of string and pulley and friction in pulley )

View SolutionTwo blocks each having mass m is attached to each other with a spring having force constant k. The system is placed on a rough horizontal surface having coefficient of friction μ. The maximum initial compression, that can be given to the spring so that when released the blocks do not move is
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View Solution
