Doubtnut Promotions Sticky

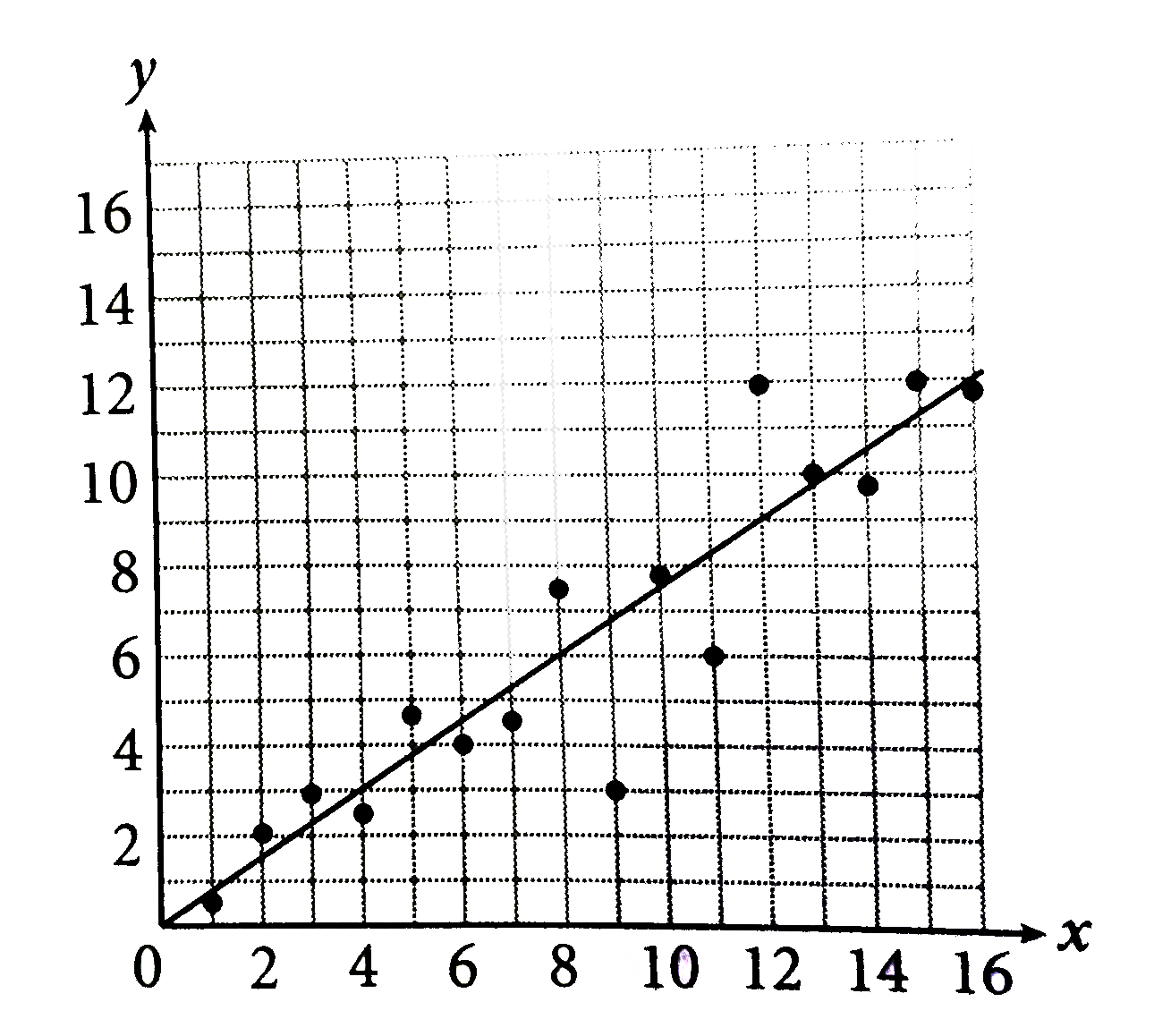
By what percent does the y-coordinate of the data point (12,12) deviate from the y-value predicted by the line of best fit for an x-valued of 12? (Ignore the percent sign and grid your response to the nearest percent.)
By what percent does the y-coordinate of the data point (12,12) deviate from the y-value predicted by the line of best fit for an x-valued of 12? (Ignore the percent sign and grid your response to the nearest percent.)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:33

The point (12,12) is 3 full girid lines away from the line of best fit, which goes through (12,9).To find percent difference between the expected and actual y-values, use the percent change formula. Note that the phrasing of the questin indicates that the orginal value of use is 9, the y-value on the line of best fit: 12−99×100%=39×100%=33.3%.
Grid in 33.

|
Updated on:21/07/2023
Class 12MATHSLINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The distance of the point (1,-1) from the line 12(x-6) = 5( y+2) is

    A(a) 5 units
    B(b) 25 units
    C(c) 52 units
    D(d) 254 units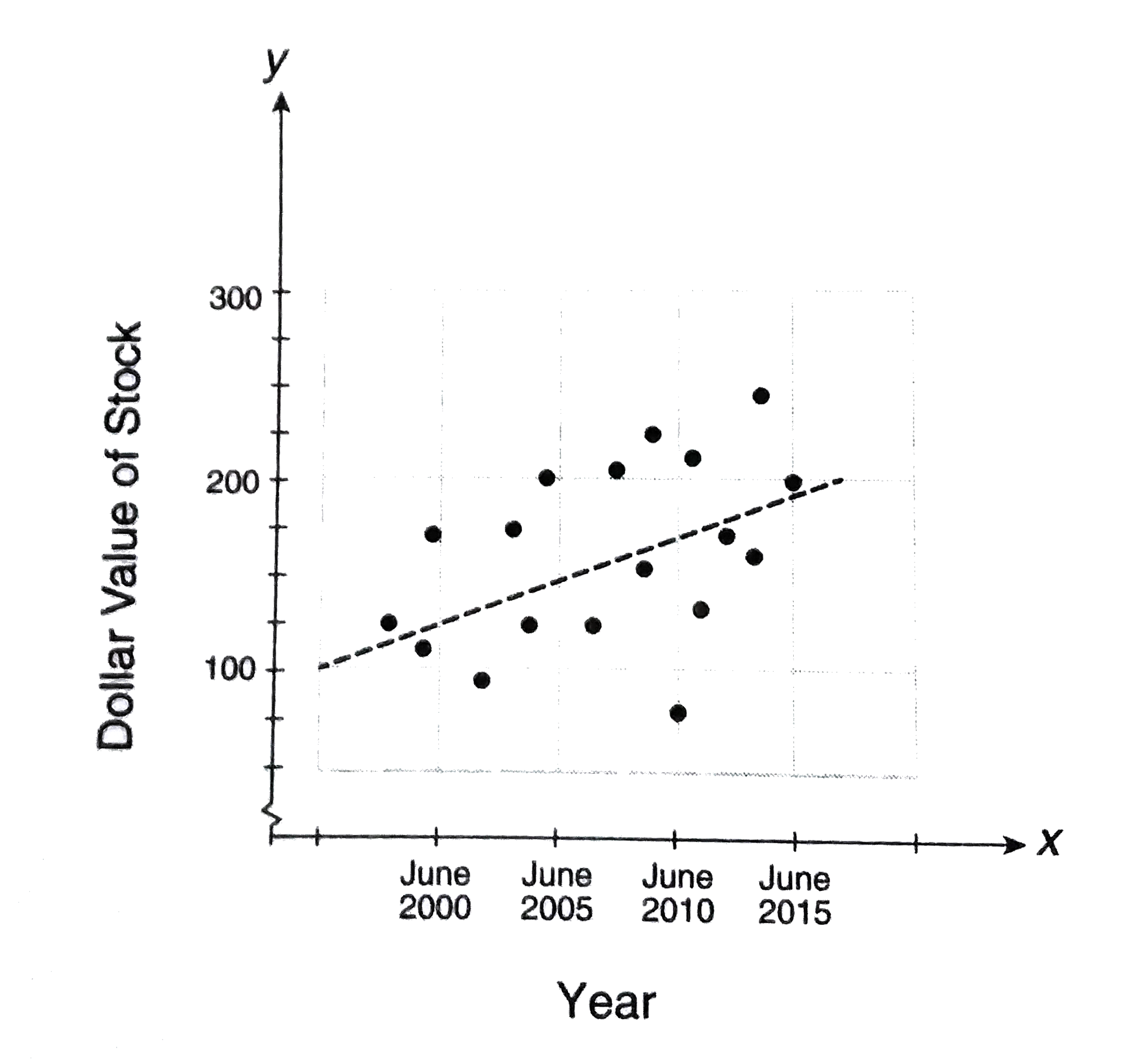
  • Question 2 - Select One

    ocr_image
    The graph above shows how the value of a stock has increased over time. The line of best fit is shown.
    a. The value of the stock increased from June 2000 to Jone 2005 by approcimately what percent?

    A0.16
    B0.2
    C0.25
    D0.28