In the xy-coordinate plane, the graph of y=5x2−12x intersects the grphs of y=−2 at points (0,0) and (a,b). What is the value of a ?
The correct Answer is:2
To find the value of a where the graphs of y=5x2−12x and y=−2 intersect, we can follow these steps:
Step 1: Set the equations equal to each other
We start by setting the two equations equal to each other since at the points of intersection, the y-values will be the same.
5x2−12x=−2
Step 2: Rearrange the equation
Next, we rearrange the equation to set it to zero:
5x2−12x+2=0
Step 3: Use the quadratic formula
Now, we will use the quadratic formula to solve for x. The quadratic formula is given by:
x=−b±√b2−4ac2a
In our equation, a=5, b=−12, and c=2.
Step 4: Calculate the discriminant
First, we calculate the discriminant b2−4ac:
b2−4ac=(−12)2−4⋅5⋅2=144−40=104
Step 5: Substitute into the quadratic formula
Now we can substitute the values into the quadratic formula:
x=−(−12)±√1042⋅5=12±√10410
Step 6: Simplify √104
We can simplify √104:
√104=√4⋅26=2√26
Step 7: Substitute back to find x
Now substituting back, we have:
x=12±2√2610=6±√265
Step 8: Identify the points of intersection
The two values of x are:
x1=6+√265andx2=6−√265
Since we know one intersection point is (0,0), we need to find the other intersection point, which corresponds to a.
Step 9: Determine the value of a
The value of a is the x-coordinate of the other intersection point. We can choose either x1 or x2. Since the problem states that the points of intersection are (0,0) and (a,b), we can take:
a=6−√265
Final Answer
Thus, the value of a is:
a=6−√265
---
We start by setting the two equations equal to each other since at the points of intersection, the y-values will be the same.
Next, we rearrange the equation to set it to zero:
Now, we will use the quadratic formula to solve for x. The quadratic formula is given by:
First, we calculate the discriminant b2−4ac:
Now we can substitute the values into the quadratic formula:
We can simplify √104:
Now substituting back, we have:
The two values of x are:
The value of a is the x-coordinate of the other intersection point. We can choose either x1 or x2. Since the problem states that the points of intersection are (0,0) and (a,b), we can take:
Thus, the value of a is:
Topper's Solved these Questions
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SOLVING QUADRATICS BY FACTORING
1 Videos
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - CLASSIC QUADRATICS
1 Videos
- QUADRATICSBOOK - KAPLANCHAPTER - QUADRATICSEXERCISE - SYSTEMS OF QUADRATIC AND LINEAR EQUATIONS
1 Videos
- PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES BOOK - KAPLANCHAPTER - PAIRED PASSAGES AND PRIMARY SOURCE PASSAGES EXERCISE - HOW MUCH HAVE YOU LEARNED
11 Videos
- SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESBOOK - KAPLANCHAPTER - SAT MATH: TIMING ANS SECTION MANAGEMENT STRATEGIESEXERCISE - TRY ON YOU OWN
5 Videos
Similar Questions
Knowledge Check
The function f is defined by f(x)=x4−4x4−x2+cx−12 , where c is a constant.In the xy-plane, the graph of f intersects the x-axis in the four points (-2,0), (1,0), (p,0), and (q,0). What is the value of c ?
A16B−16CpqDqpIn the xy-plane, the parabola with equation y=(x−11)2 intersects the line with equation y = 25 at two points, A and B. What is the length of ¯¯¯¯¯¯AB ?
A10B12C14D16What is the y - coordinate of the point at which the graph of y = 2 sin x - cos 2 x intersects the y - axis ?
A−2B−1C0D1
g(x)=x4−kx3+13x2−12x+4
The function g is defined above, and k is a constant. In the xy- plane, the graph of g intersects the y - axis at (0,4) and intersects the x - axis at (1,0) and (2,0). What is the value of k?
View Solution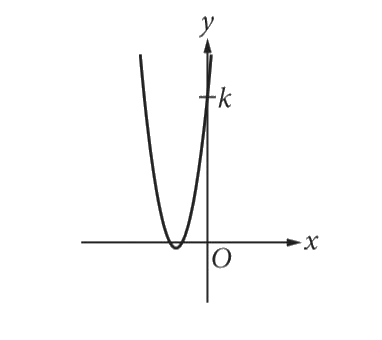
The graph of y=2x2+10x+12 is shown. If the graph crosses the y -axis at the point ( 0, k) , what is the value of k ?
View Solution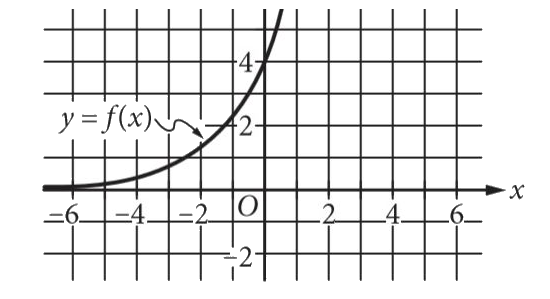
The graph of y = f (x) is shown in the xy -plane. What is the value of f (0) ?
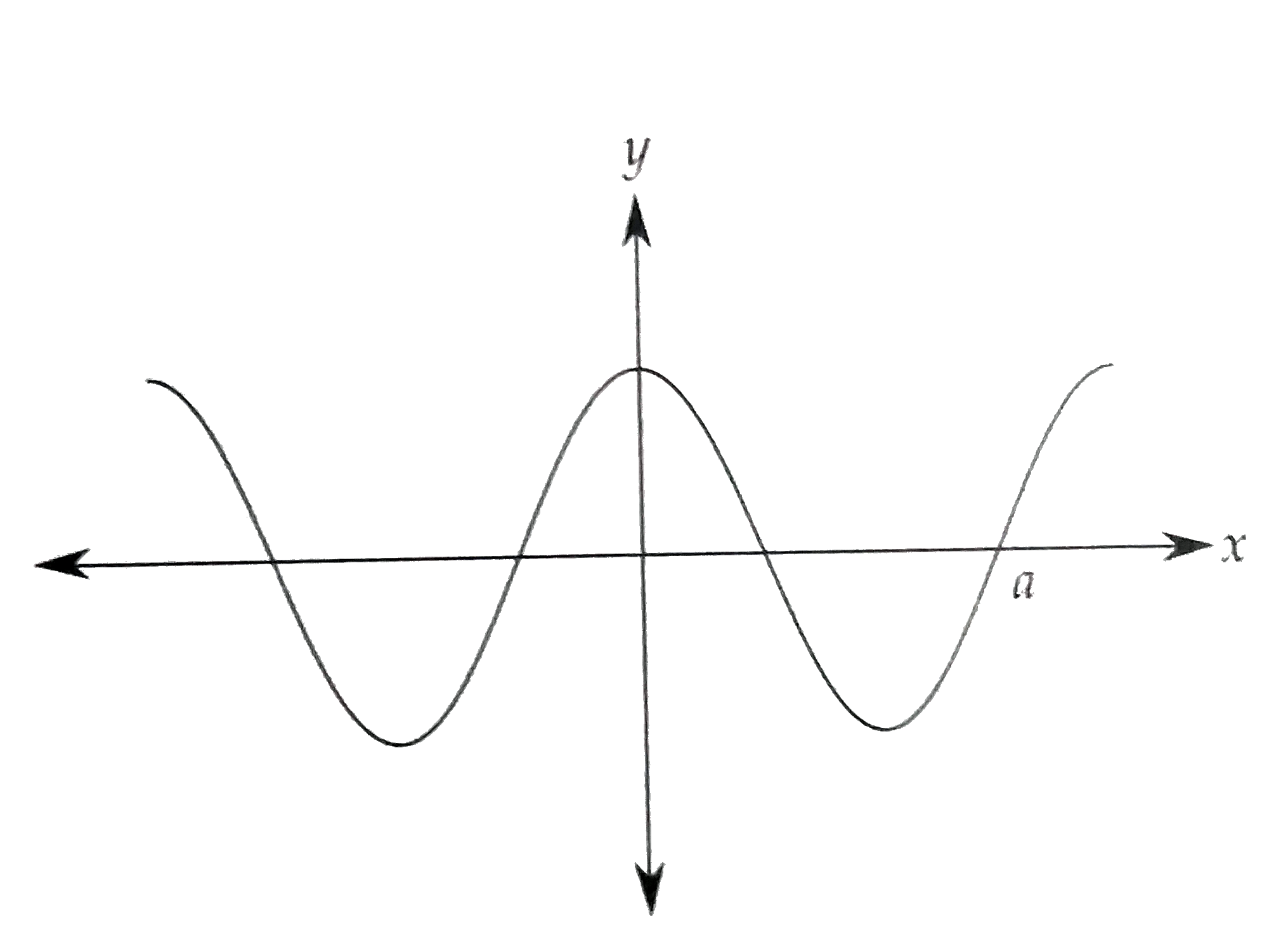
View SolutionThe graph of y=cos.x2 is shown in Figure Point a has coordinates (t, 0). What is the value of t in radians ?
View SolutionIn how many points graph of y=x3−3x2+5x−3 intersect the x-axis?
View Solution
