Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
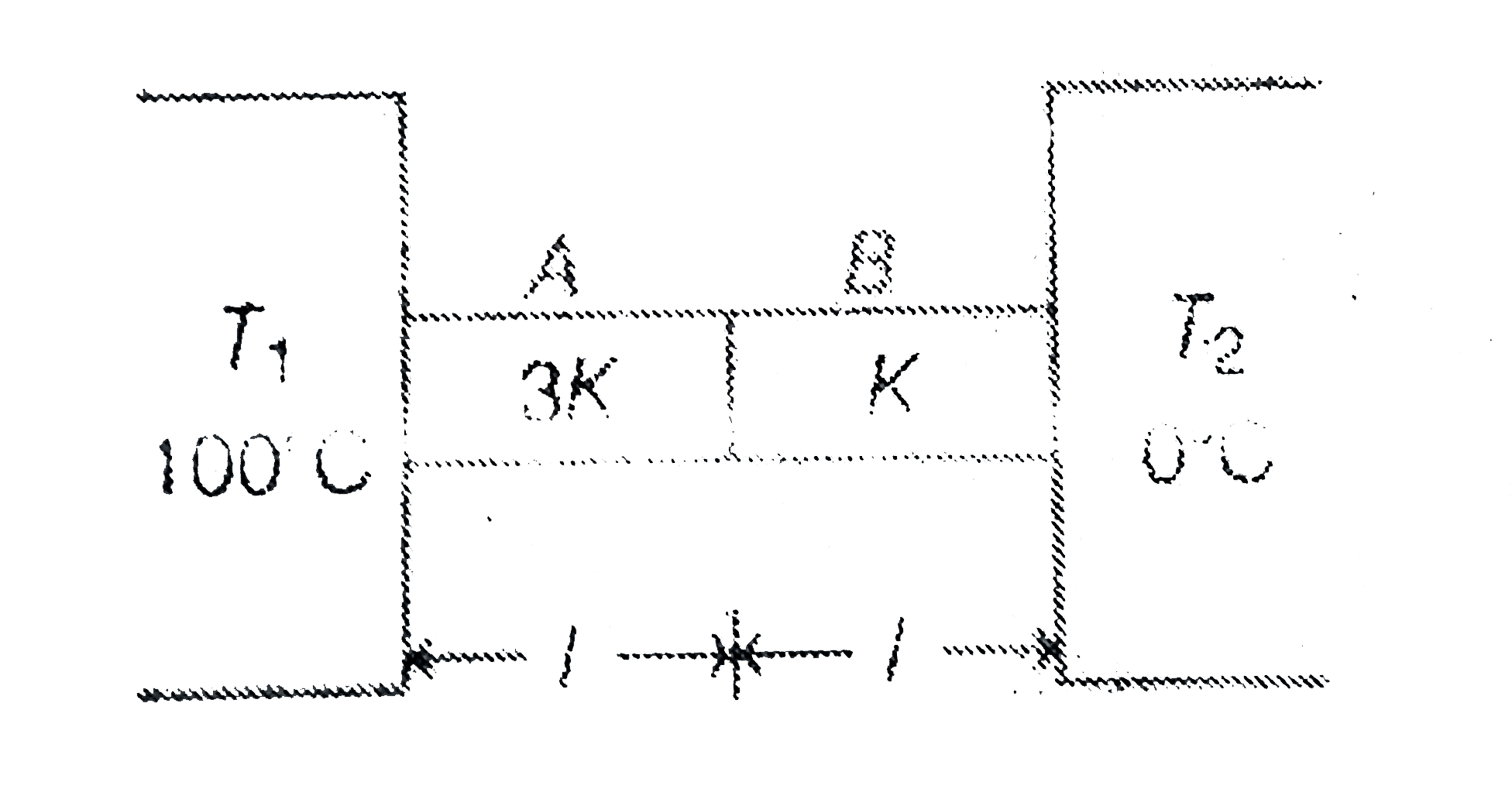
If TA and TB are the temperature drops across the rod A and B, then
TATB=31
TATB=13
TATB=34
TATB=43
The correct Answer is:B
Step by step video, text & image solution for Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T_(1)=100^(@)C) and a sink (T_(2)-0^(@)C) as shown in figure. The rod is laterally insulated. If T_(A) and T_(B) are the temperature drops across the rod A and B, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
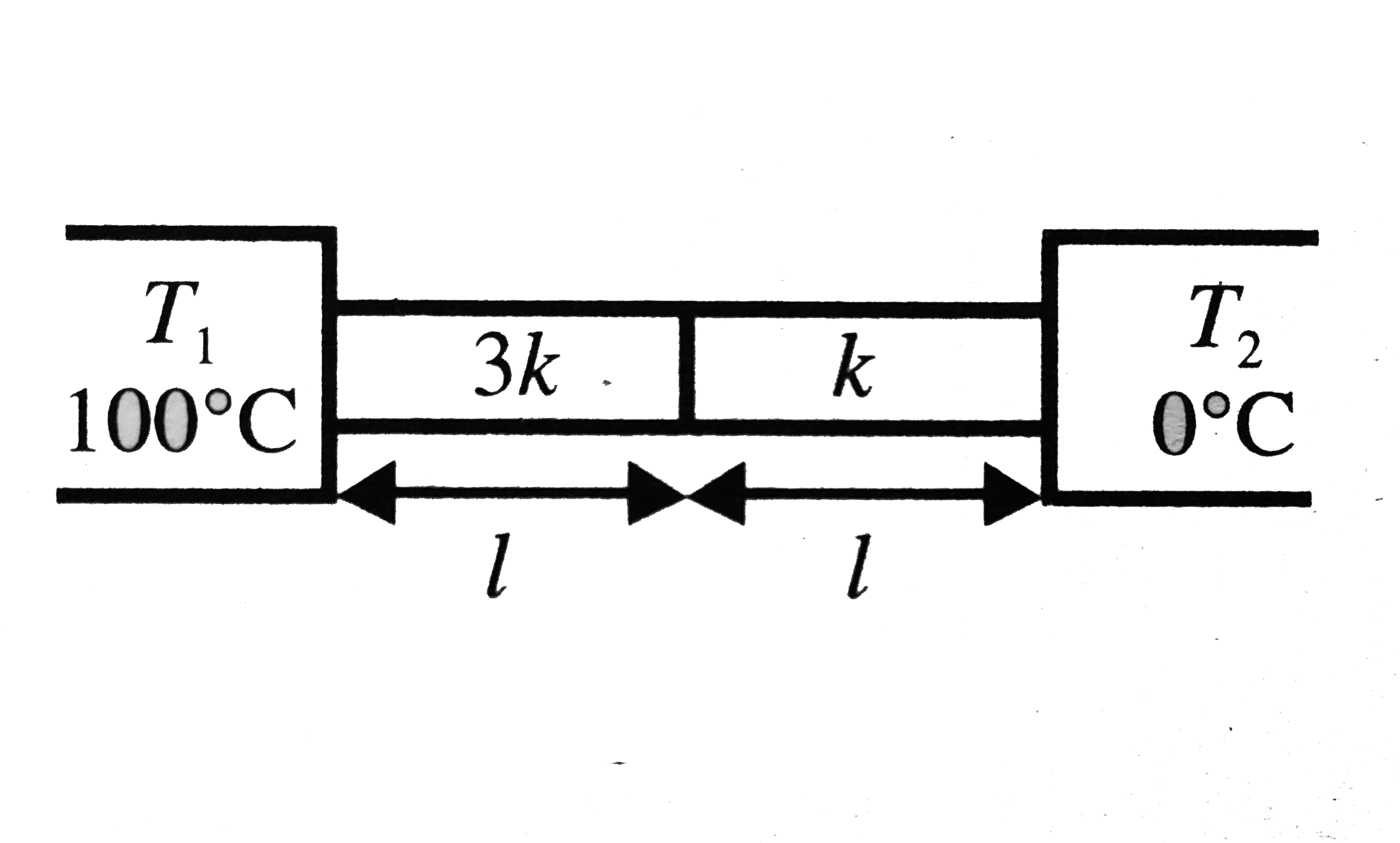
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionThree rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.

View Solution
Knowledge Check
Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
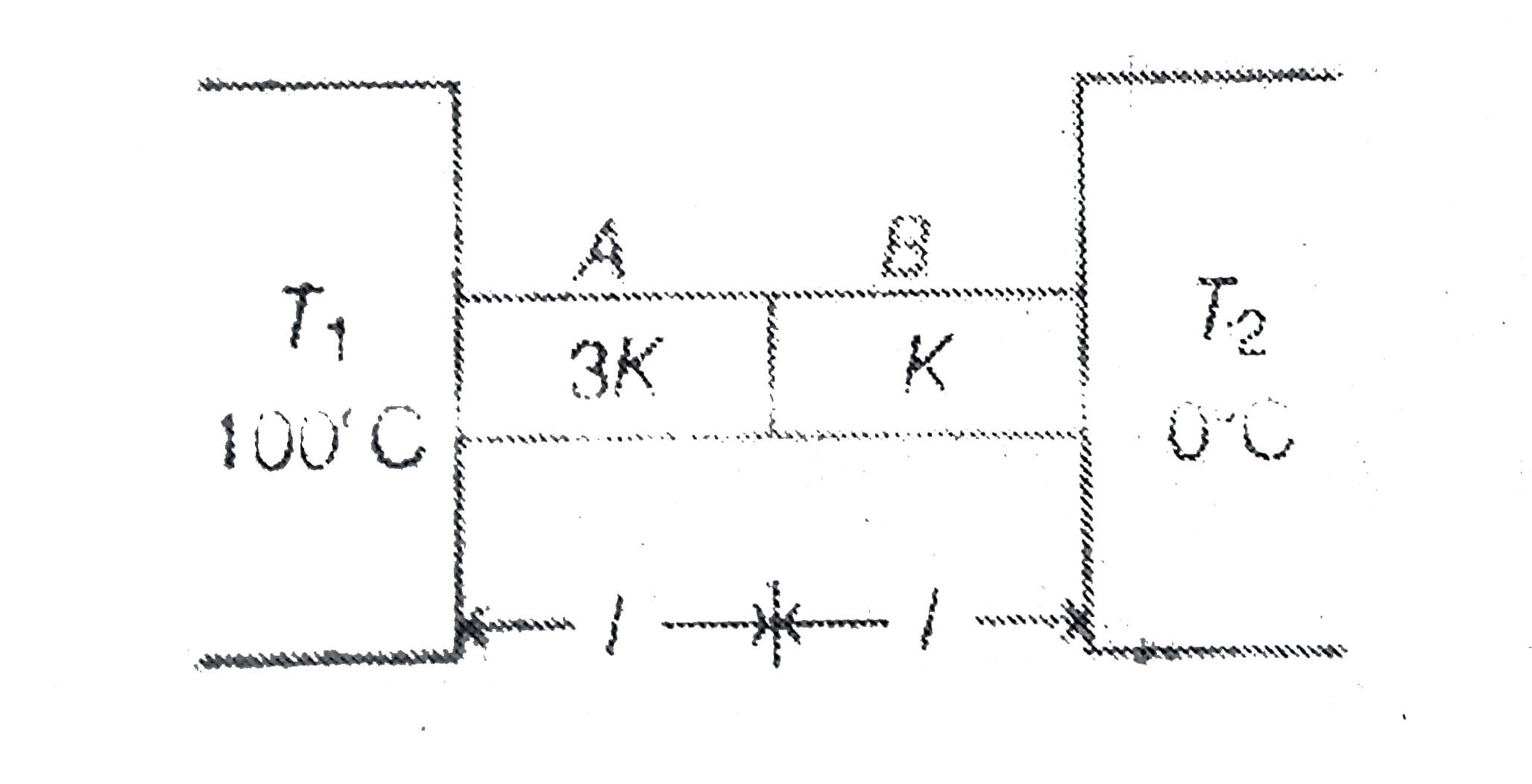
If GA and GB are the temperature gradients across the rod A and B, thenAGAGB=34BGAGB=13CGAGB=34DGAGB=43Two rods A and B of same cross sectional are A and length l connected in series between a source
(T1=100∘C) and a sink (T2=0∘C) as shown in The rod is laterally insulated

If AA and TB are the temperature drops across temperature gradients the rod A and B then .ATAAB=31BTATB=13CTATB=34DTATB=43Two rods A and B of same cross-sectional area A and length l are connected in series between a source (T1=100∘C) and a sink (T2−0∘C) as shown in figure. The rod is laterally insulated.
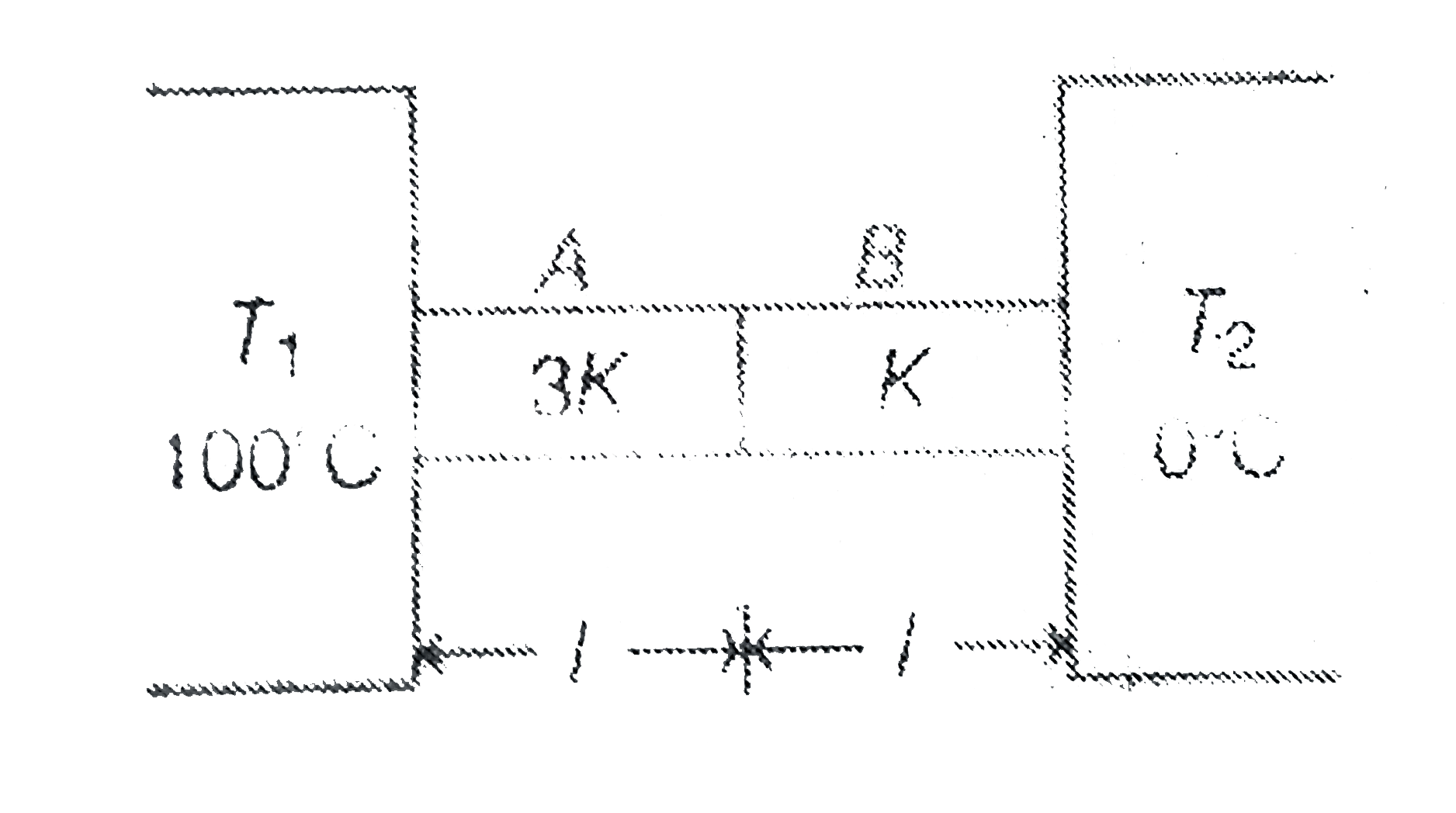
The ratio of the thermal resistance of the rods isARARB=13BRARB=3CRARB=34DRARB=43
Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionTwo rods A and B of same cross sectional are A and length l connected in series between a source
(T1=100∘C) and a sink (T2=0∘C) as shown in The rod is laterally insulated

The ratio of thermal resistance of the rod is .
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
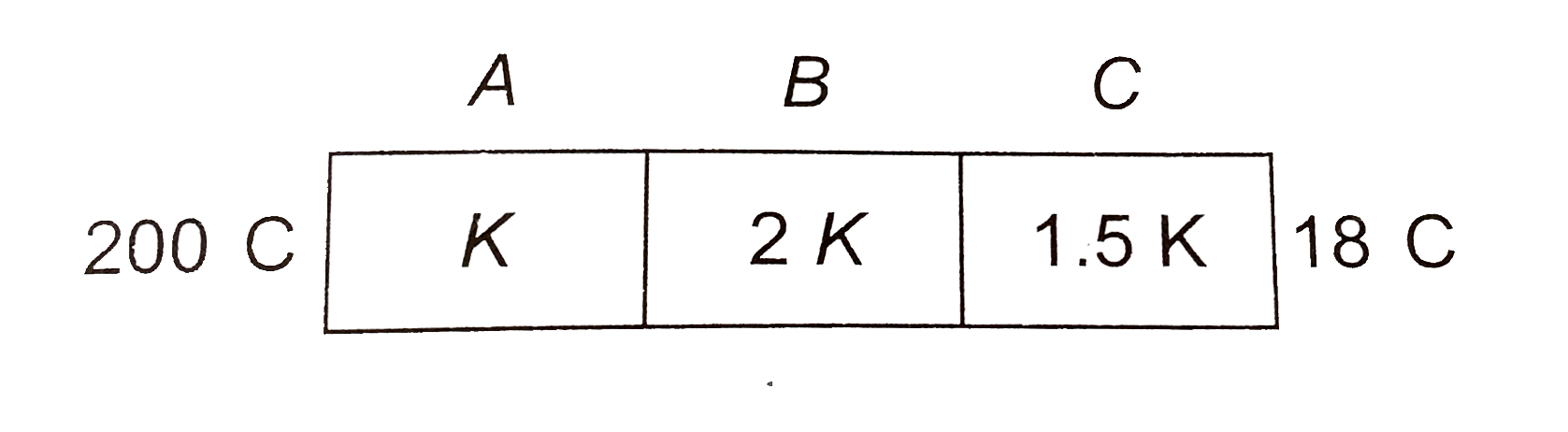
View Solution
Two ends of a rod of uniform cross sectional area are kept at temperature 3T0 and T0 as shown. Thermal conductivity of rod varies as k=αT, (where α is a constant and T is absolute temperature). In steady state, the temperature of the middle section of the rod is
View SolutionThree rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be

View Solution

