A metal block is placed in a room which is at 10∘C for long time. Now it is heated by an electric heater of power 500 W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C . (Assume Newtons Law of cooling to be valid)
What is the heat capacity of the block?
50J/∘C
100J/∘C
150J/∘C
200J/∘C
The correct Answer is:D
Step by step video, text & image solution for A metal block is placed in a room which is at 10^(@)C for long time. Now it is heated by an electric heater of power 500 W till its temperature becomes 50^(@)C. Its initial rate of rise of temperature is 2.5^(@)C//sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50^(@)C . (Assume Newtons Law of cooling to be valid) What is the heat capacity of the block? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A metal block is placed in a room which is at 10∘C. It is heated by an electric heater of power 500W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C. (Assume Newtons Law of cooling to be valid)
(i) What is the heat capacity of the block ?
(ii) What is the rate of cooling of block at 50∘C if the 100W heater is also switched off ?
(iii) What is the heat radiated per second when the block was 30∘C ?
View SolutionA metal block is placed in a room which is at 10∘C for long time. Now it is heated by an electric heater of power 500W till its temperature becomes 50∘C Its initial rate of rise of temperature is 2.5∘C/sec The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C The heat radiated per second when the block was 30∘C is given as α watt. Find the value of (α10) (Assume Newton's law of cooling to be valid .
View Solution
Knowledge Check
A metal block is placed in a room which is at 10∘C for long time. Now it is heated by an electric heater of power 500 W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C . (Assume Newtons Law of cooling to be valid)
What is the rate of cooling of block at 50∘C if the 100W heater is also switched off?A5∘C/sB0.5∘C/sC1∘C/sD0.1∘C/sA system S receives heat continuously from an electric heater of power 10W. The temperature of S becomes constant at 50∘C when the surrounding temperature is 20∘C. After the heater is switched off, S cools from 35.1∘C to 34.9∘C in 1minute. the heat capacity of S is
A100J/∘CB300J/∘CC750J/∘CD1500J/∘C
A metal block of heat capacity 90J/.∘C placed in a room at 25∘C is heated electrically. The heater is switched off when the temperature reaches 35∘C. The temperature of the block rises at the rate of 2∘C/s just after the heater is switched on and falls at the rate of 0.2∘C/s just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is 30∘C. (d) Assuming that the power radiated at 30∘C respresents the average value in the heating process, find the time for which the heater was kept on.
View SolutionHeat is generated continuously in an electric heater, but its temperature becomes constant after some time. Why?
View SolutionA metal block of heat capacity 90J/.∘C placed in a room at 25∘C is heated electrically. The heater is switched off when the temperature reaches 35∘C. The temperature of the block rises at the rate of 2∘C/s just after the heater is switched on and falls at the rate of 0.2∘C/s just after the heater is switched off. Assume Newton's law of cooling to hold (a) Find the power of the heater. (b) Find the power radiated by the block just after the heater is switched off. (c ) Find the power radiated by the block when the temperature of the block is 30∘C. (d) Assuming that the power radiated at 30∘C respresents the average value in the heating process, find the time for which the heater was kept on.
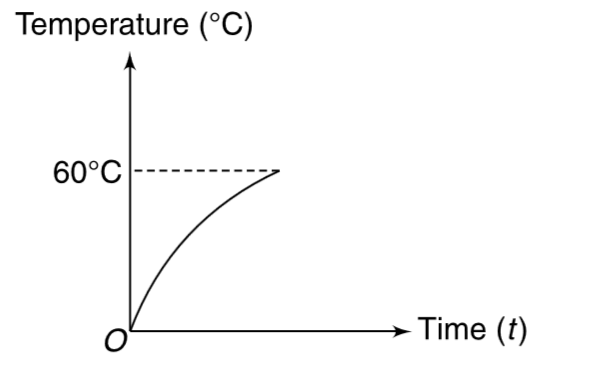
View SolutionA block is kept in a room which is at 20∘C. To raise the temperature of the block, heat is given to it at a constant rate of 600 watt (using an electric heater). The temperature of the block rises with time as shown in the graph. The slope of the graph at time t=0 is 3∘Cs−1. Once the temperature rises to 60∘C, the heater is switched off and another heater is switched on to maintain the temperature of the block at 60∘C. This new heater supplies heat at a constant rate of 100 watt. Assume that heat capacity of the block remains constant for the range of temperature involved.
(a) Explain why the slope of the given graph is decreasing with time.
(b) Calculate the heat capacity of the block.
(c) If the 100 W heater is also switched off, what will be initial rate of cooling of the block?
(d) Assuming that rate of heat loss by the block to the surrounding is proportional to difference in its temperature with surrounding, calculate the heat radiated per second by the block when it was at 30∘C.
View SolutionA metal block with a heater in it is placed in a room at temperature 293 K. When the heater is switched on it is observed that the temperature of the block rises at the rate of 2∘C/s and when its temperature rises to 30∘C, it is switched off. Just after when heater is switched off, it is observed that the block cools at 0.2∘C/s. If Newton's law of cooling is assumed to be valid, find the power of the heater. Also find the thermal power radiated by the block when it was at 30∘C and at 25∘C. Given that the heat capacityof the block is 80J/∘C.
View SolutionAssertion: Heat is generated continoulsy in an electric heater but its temperature becomes constant after some time.
Reason:- At the stage when heat produced in heater is equal to the heat dissipated to its surrounding the temperature of heater becomes constant.
View Solution

