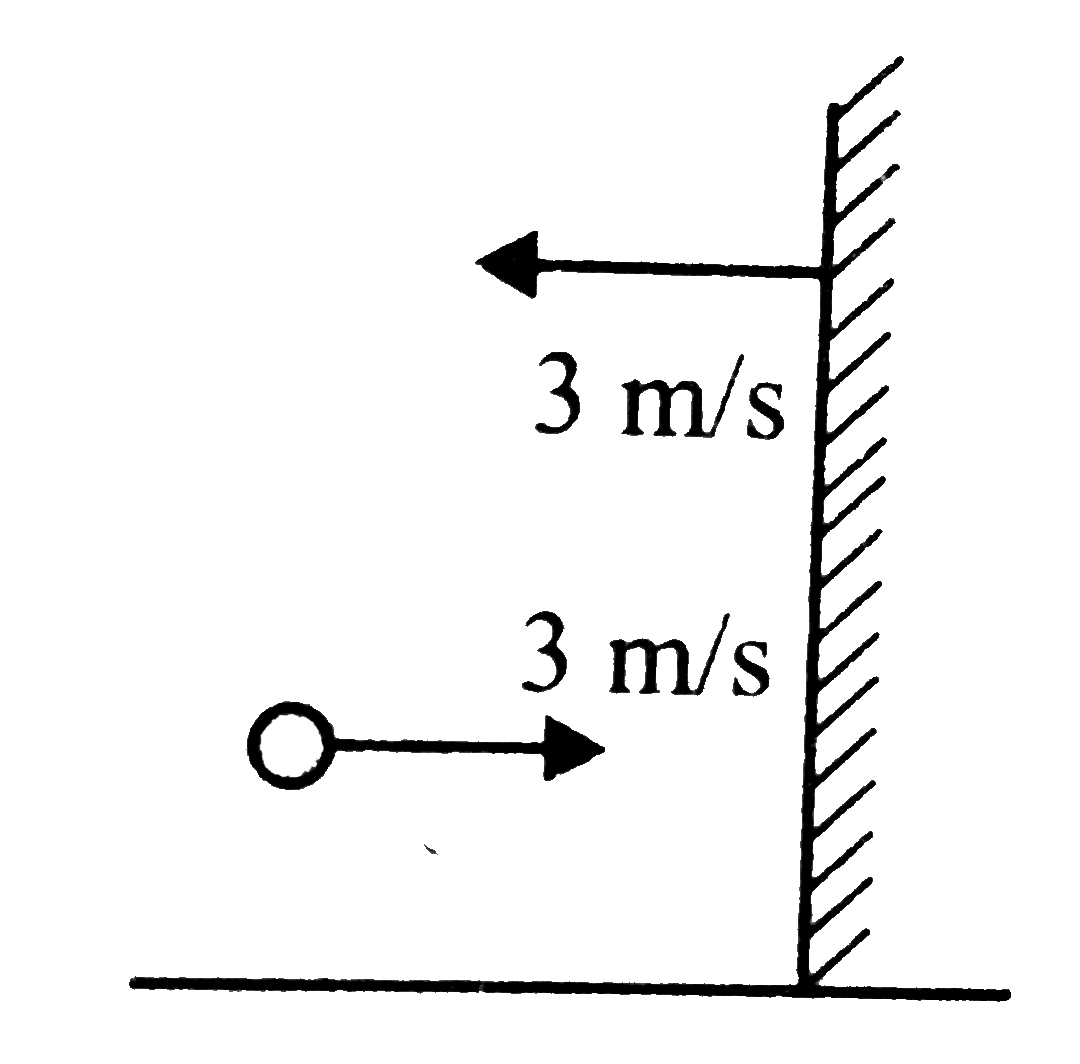
A ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

The speed of wall will not change after the collision. So, let v be the velocity of the ball after collision in the direction shown in figure, Since, collision is elastic (e=1),
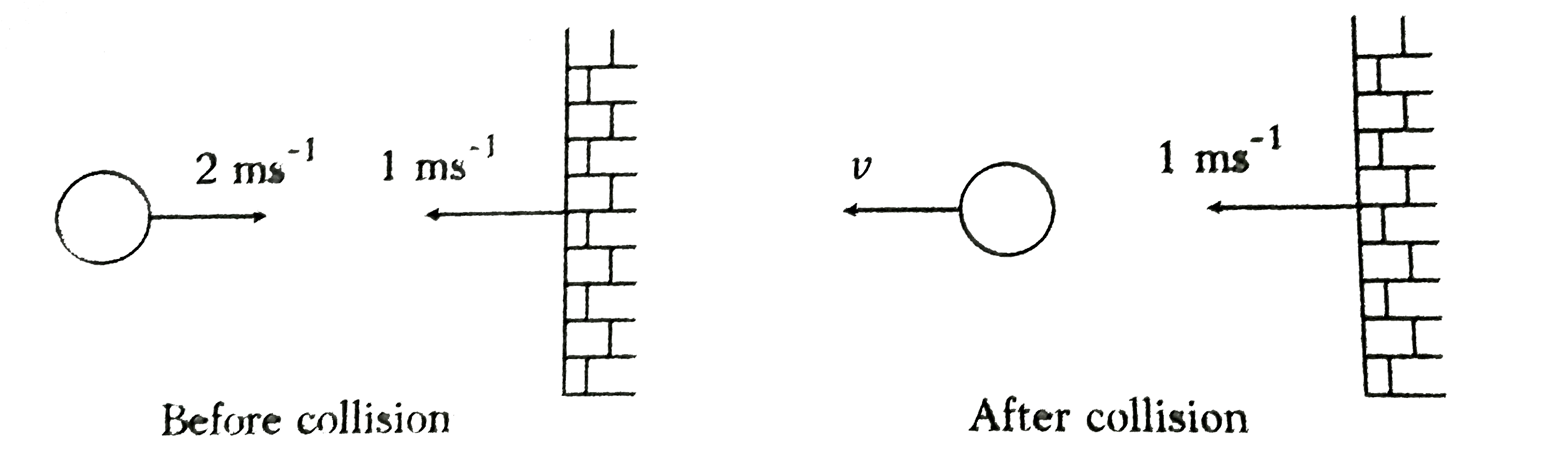
separation speed = approach speed
or v−1=2+1orv=ms−1
Topper's Solved these Questions
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Check points
Explore 50 Videos
- CENTRE OF MASSBook:DC PANDEYChapter:CENTRE OF MASSExercise:Taking it together
Explore 73 Videos
- CALORIMETRY AND HEAT TRANSFERBook:DC PANDEYChapter:CALORIMETRY AND HEAT TRANSFERExercise:Medical entrance s gallery
Explore 38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBook:DC PANDEYChapter:CENTRE OF MASS, IMPULSE AND MOMENTUMExercise:Comprehension type questions
Explore 15 Videos
Similar Questions
A ball of mass m moving with speed v towards the right strikes a wall moving towards the left with speed u. Find the change in the K.E. of the ball if the collision is elastic.
View SolutionThe two balls shown in figure are identical the first moving at a speed v towards right and the second staying at rest. The wall at the extreme right is fixed. Assume all collisions to be elastic. Show that the speeds of the balls remain unchanged after all the collisions have taken place.
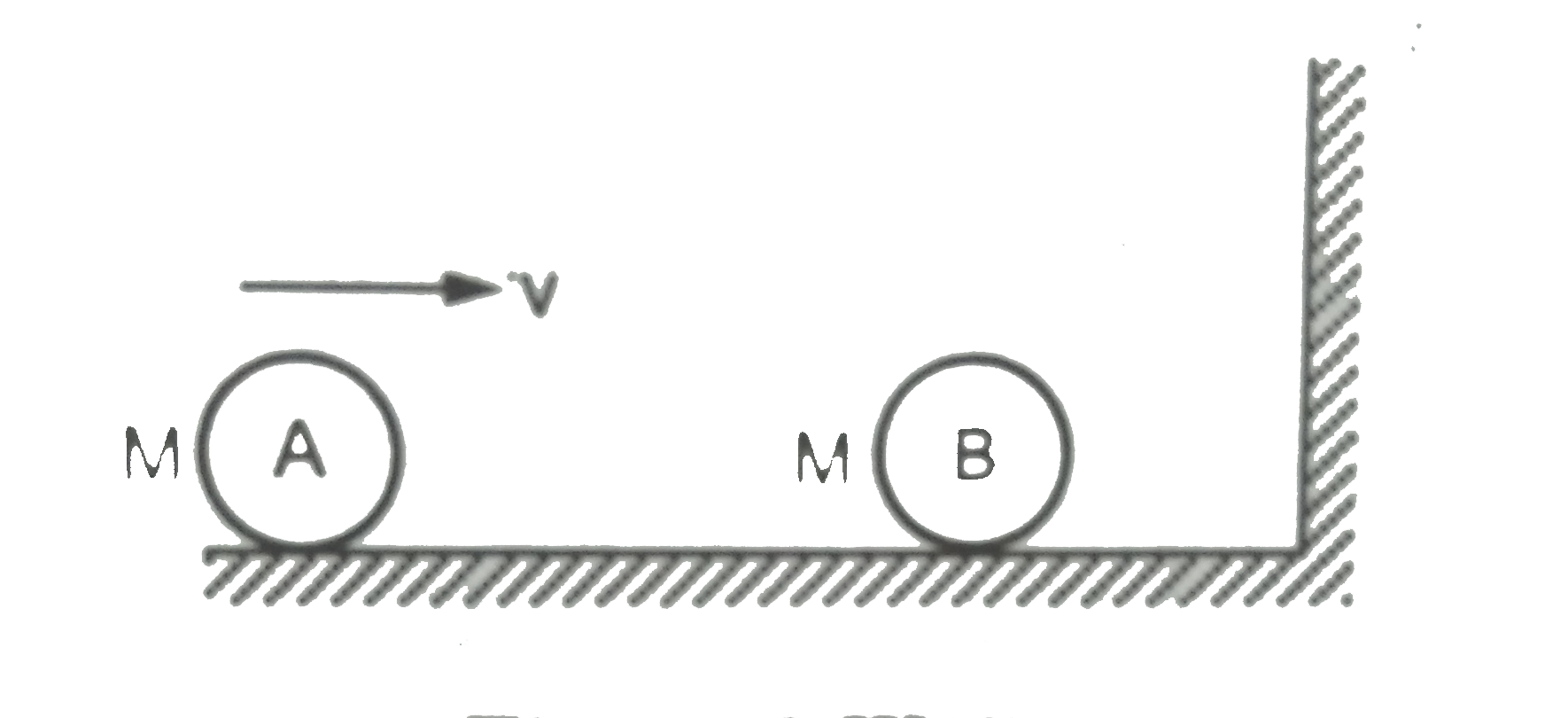
View Solution
Knowledge Check
A wall moving with velocity 2cms−1 towards the ball and ball is moving towards the wall with a velocity 10cms−1. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in cms−1.
A12B8C14D16A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
AThe average elastic force acting on the ball is [m(u+v)]/△tBThe average elastic force acting on the ball is [2m(u+v)]/△tCThe kinetic energy of the ball increases by 2mu(u+v).DThe kinetic energy of the ball remains the same after the collision.A ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
AThe average elastic force acting on the ball is m(u+v)ΔtBThe average elastic force acting on the ball is 2m(u+v)ΔtCthe kinetic energy of the ball increases by 2mu (u + v)Dthe kinetic energy of the ball does not change
A particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
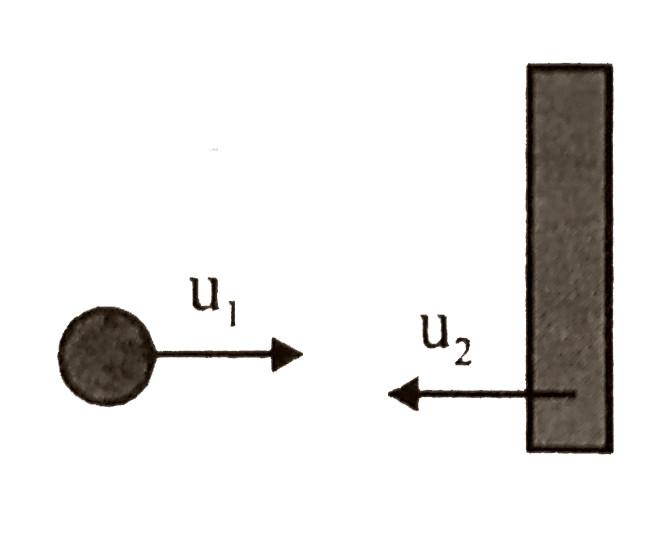
View SolutionA ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
View SolutionA ball of mass 10 kg is moving with a velocity of 10 m / s . It strikes another ball of mass 5 kg which is moving in the same direction with a velocity of 4 m / s . If the collision is elastic, their velocities after the collision will be, respectively
View SolutionRod can rotate about hinge point 'P'. A ball of mass 'm' is projected with a velocity 5v0 in a gravity free space as shown in figure. Collision between the rod and the ball is perfectly elastic. Then find the magnitude of velocity of ball after the collision ( neglect the friction between the ball and the rod during the collision ).
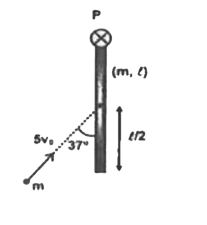
View SolutionA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
View Solution