A ball of mass m moving with speed v towards the right strikes a wall moving towards the left with speed u. Find the change in the K.E. of the ball if the collision is elastic.
To solve the problem of finding the change in kinetic energy of a ball after an elastic collision with a wall, we can follow these steps:
Step 1: Understand the Initial Conditions
- We have a ball of mass m moving to the right with speed v.
- The wall is moving to the left with speed u.
Step 2: Determine the Initial Kinetic Energy of the Ball
The initial kinetic energy KEinitial of the ball can be calculated using the formula:
KEinitial=12mv2
Step 3: Find the Final Velocity of the Ball After Collision
In an elastic collision, the relative velocity of separation is equal to the relative velocity of approach. We can express this mathematically as:
vball,final=vball,initial+(vwall,final−vwall,initial)
Here, the wall is assumed to have a very large mass compared to the ball, so its velocity after the collision can be approximated as −u (it continues moving left). Therefore:
vball,final=v+u
Step 4: Calculate the Final Kinetic Energy of the Ball
The final kinetic energy KEfinal of the ball after the collision is:
KEfinal=12m(v+u)2
Step 5: Calculate the Change in Kinetic Energy
The change in kinetic energy ΔKE is given by:
ΔKE=KEfinal−KEinitial
Substituting the expressions for kinetic energy:
ΔKE=12m(v+u)2−12mv2
Step 6: Simplify the Expression
Now, we can factor out 12m:
ΔKE=12m((v+u)2−v2)
Expanding (v+u)2:
(v+u)2=v2+2vu+u2
Thus,
ΔKE=12m(v2+2vu+u2−v2)
This simplifies to:
ΔKE=12m(2vu+u2)
Final Result
The change in kinetic energy of the ball after the elastic collision with the wall is:
ΔKE=m(vu+12u2)
---
- We have a ball of mass m moving to the right with speed v.
- The wall is moving to the left with speed u.
The initial kinetic energy KEinitial of the ball can be calculated using the formula:
KEinitial=12mv2
In an elastic collision, the relative velocity of separation is equal to the relative velocity of approach. We can express this mathematically as:
vball,final=vball,initial+(vwall,final−vwall,initial)
Here, the wall is assumed to have a very large mass compared to the ball, so its velocity after the collision can be approximated as −u (it continues moving left). Therefore:
vball,final=v+u
The final kinetic energy KEfinal of the ball after the collision is:
KEfinal=12m(v+u)2
The change in kinetic energy ΔKE is given by:
ΔKE=KEfinal−KEinitial
Substituting the expressions for kinetic energy:
ΔKE=12m(v+u)2−12mv2
Now, we can factor out 12m:
ΔKE=12m((v+u)2−v2)
Expanding (v+u)2:
(v+u)2=v2+2vu+u2
Thus,
ΔKE=12m(v2+2vu+u2−v2)
This simplifies to:
ΔKE=12m(2vu+u2)
The change in kinetic energy of the ball after the elastic collision with the wall is:
ΔKE=m(vu+12u2)
Topper's Solved these Questions
Similar Questions
A ball of mass m moving with a speed u1 collides elasticity with another identical ball moving with velocity u2.
(a) Find the velocities of the balls after collision if the impact is direct.
(b) Find the angle between velocities after collision if they collide obliquely and u2=0
View SolutionA ball of 0.5 kg mass moving with a speed of 10m/s rebounds after strinking normally a perfectly elastic wall . Find the change in momentum of the ball.
View Solution
Knowledge Check
A ball of mass m moves with speed v and stricks a wall having infinite mass and it returns with same speed then the work done by the ball on the wall is
AZeroBmvjoe–sCm/vjoe–sDv/mjoe–sA ball of mass 0⋅2 kg moving with a speed of 30 m/s strikes a bat returns in opposite direction with speed of 90m/s . Magnitude of change in momentu,m of ball will be
AZeroB6 kg m/sC12 kg m/sD24 kg m/sA highly elastic ball moving at a speed of 3m/s approaches a wall moving towards it with a speed of 3m/s. After the collision. the speed of the ball will be
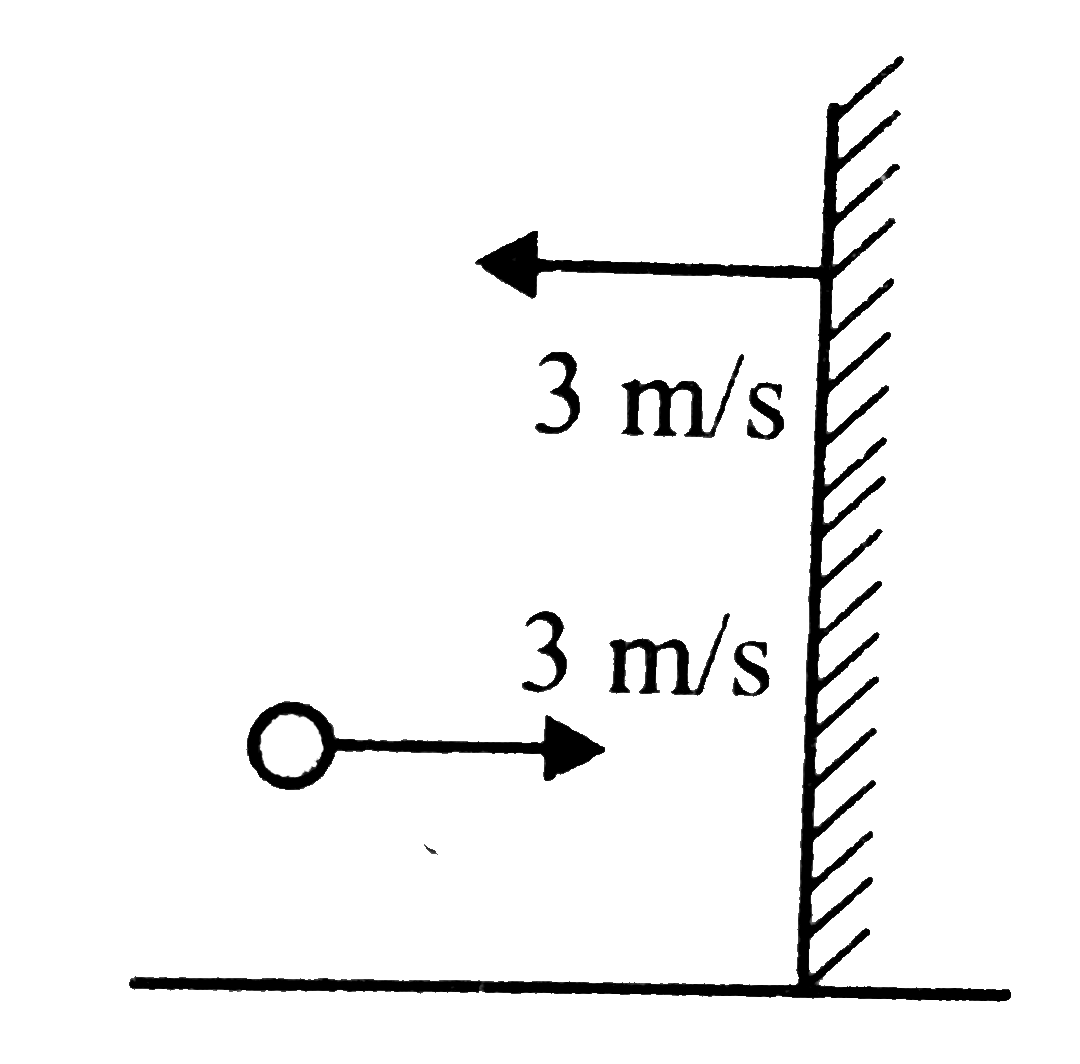 A3m/sB6m/sC9m/sDzero
A3m/sB6m/sC9m/sDzero
A ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
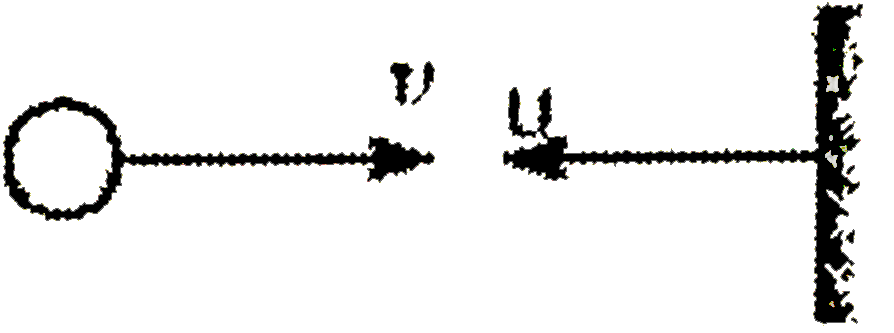
View SolutionA ball of mass 0.5kg moving with a speed of 10m/s rebounds after striking normally a perfectly elastic wall. Find the change in momentum of the ball . If contact time with the wall is 0.1s, what force is exerted by wall?
View SolutionA block of mass m moves with a speed v towards the right block which is in equilibrium with a spring attached to rigid wall. If the surface is frictionless and collisions are elastic, the frequency of collisions between the masses will be:
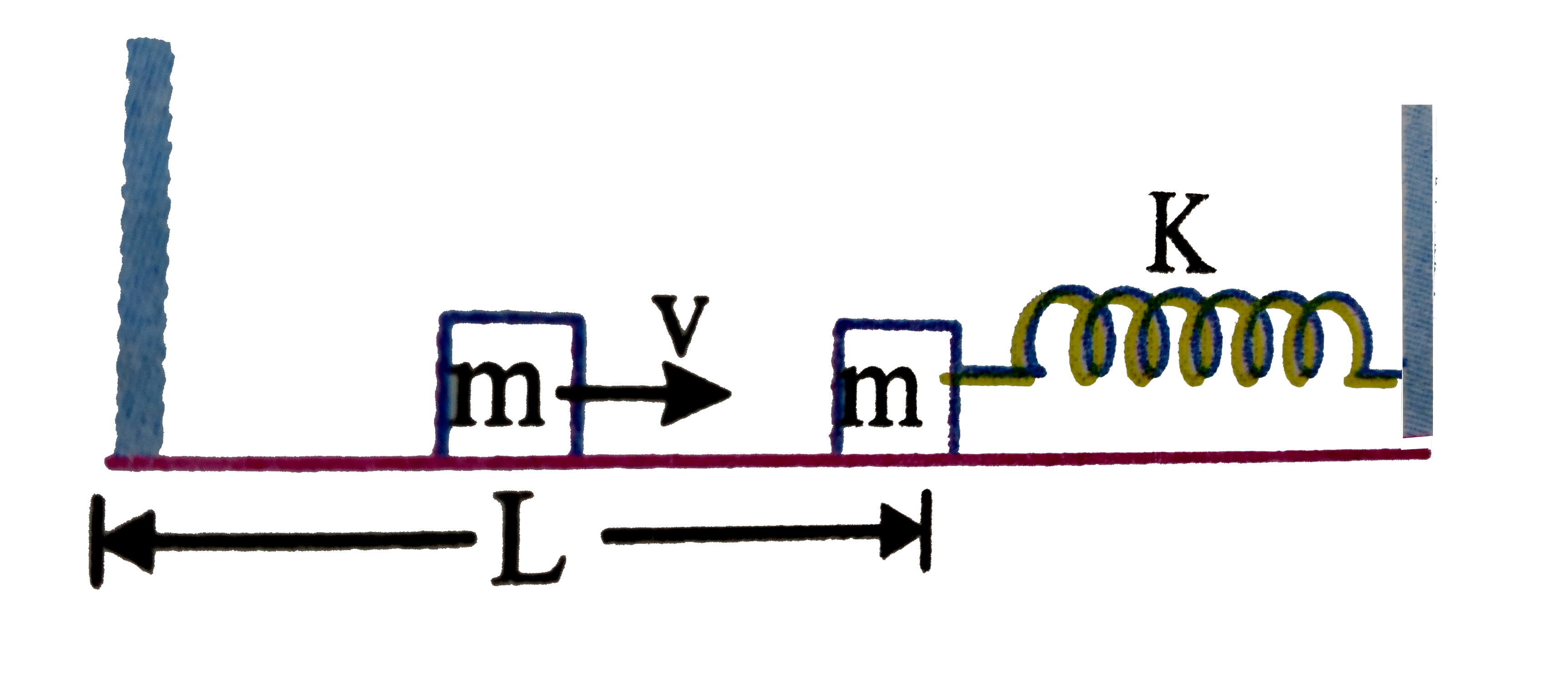
View SolutionA ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.

View SolutionA Sphere moving with velocity v strikes a wall moving towards the sphere with a velocity u. If the mass of the wall is infinitely large the work done by the wall during collision will be:
View Solution
