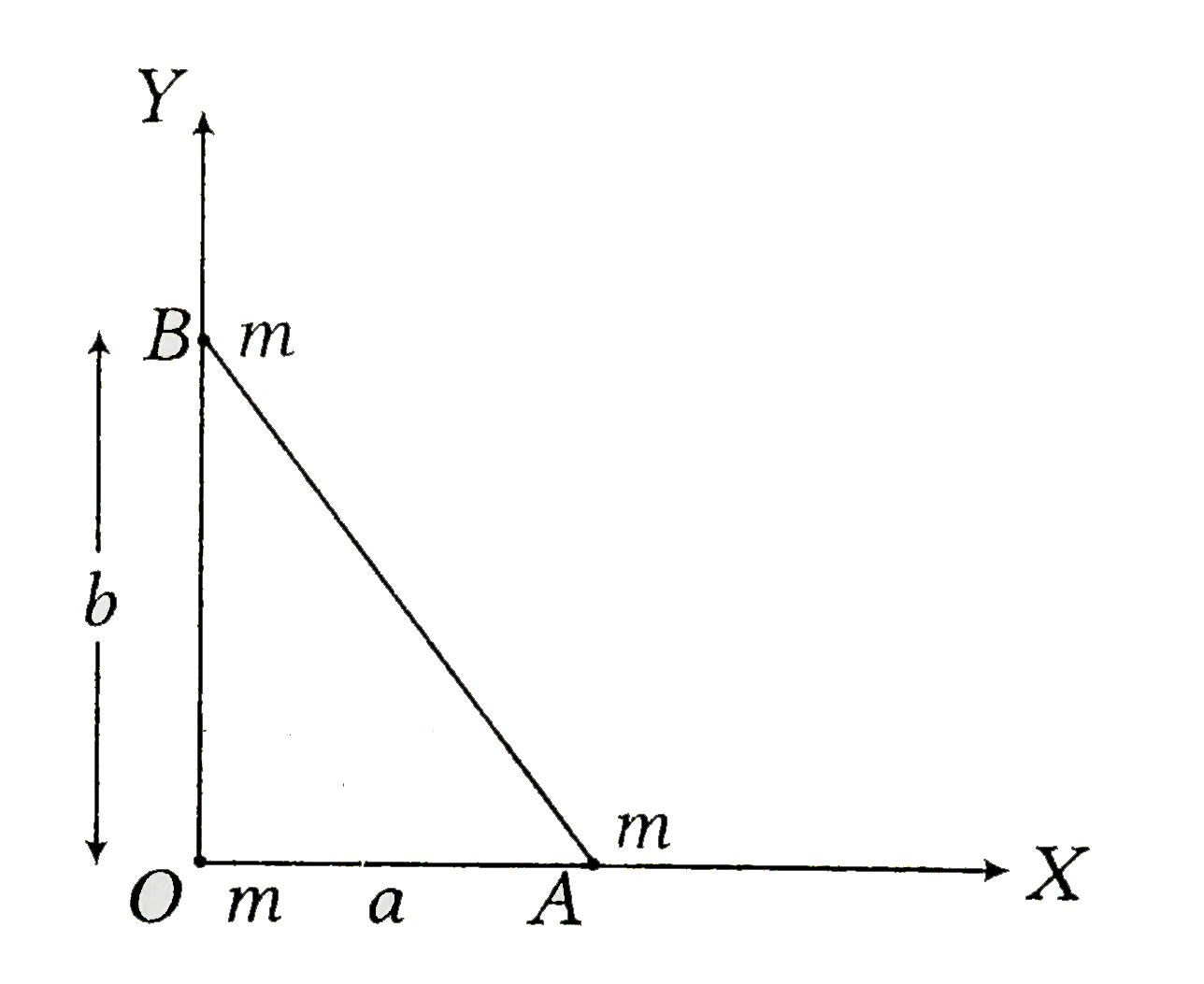
Three particles , each of mass m, are placed at the vertices of a righ

The system of vector $ˆ i, ˆ j, ˆ k$ is
Aorthogonal
Bcoplanar
Ccollinear
Dparallel
The unit vector along $ˆ i + ˆ j$ is
A $ˆ k$
B $ˆ i + ˆ j$
C $\frac{ˆ i + ˆ j}{\sqrt{2}}$
D $\frac{ˆ i + ˆ j}{2}$
A unit vector perpendicular to each of the vectors $2 ˆ i - ˆ j + ˆ k and 3 ˆ i - 4 ˆ i - ˆ k$ is
A $\frac{1}{\sqrt{3}} ˆ i + \frac{1}{\sqrt{3}} ˆ j - \frac{1}{\sqrt{3}} ˆ k$
B $\frac{1}{\sqrt{2}} ˆ i + \frac{1}{2} ˆ j + \frac{1}{2} ˆ k$
C $\frac{1}{\sqrt{3}} ˆ i - \frac{1}{\sqrt{3}} ˆ j - \frac{1}{\sqrt{3}} ˆ k$
D $\frac{1}{\sqrt{3}} ˆ i + \frac{1}{3} ˆ j + \frac{1}{\sqrt{3}} ˆ k$

Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and $ˆ i, ˆ j, ˆ k$ are unit vectors)