A body of mass (4m) is laying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each mass (m) move perpedicular to each other with equal speeds (v). Total kinetic energy generated due to explosion is

A

$m v^{2}$

B

$(\frac{3}{2}) m v^{2}$

C

$2 m v^{2}$

D

$4 m v^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

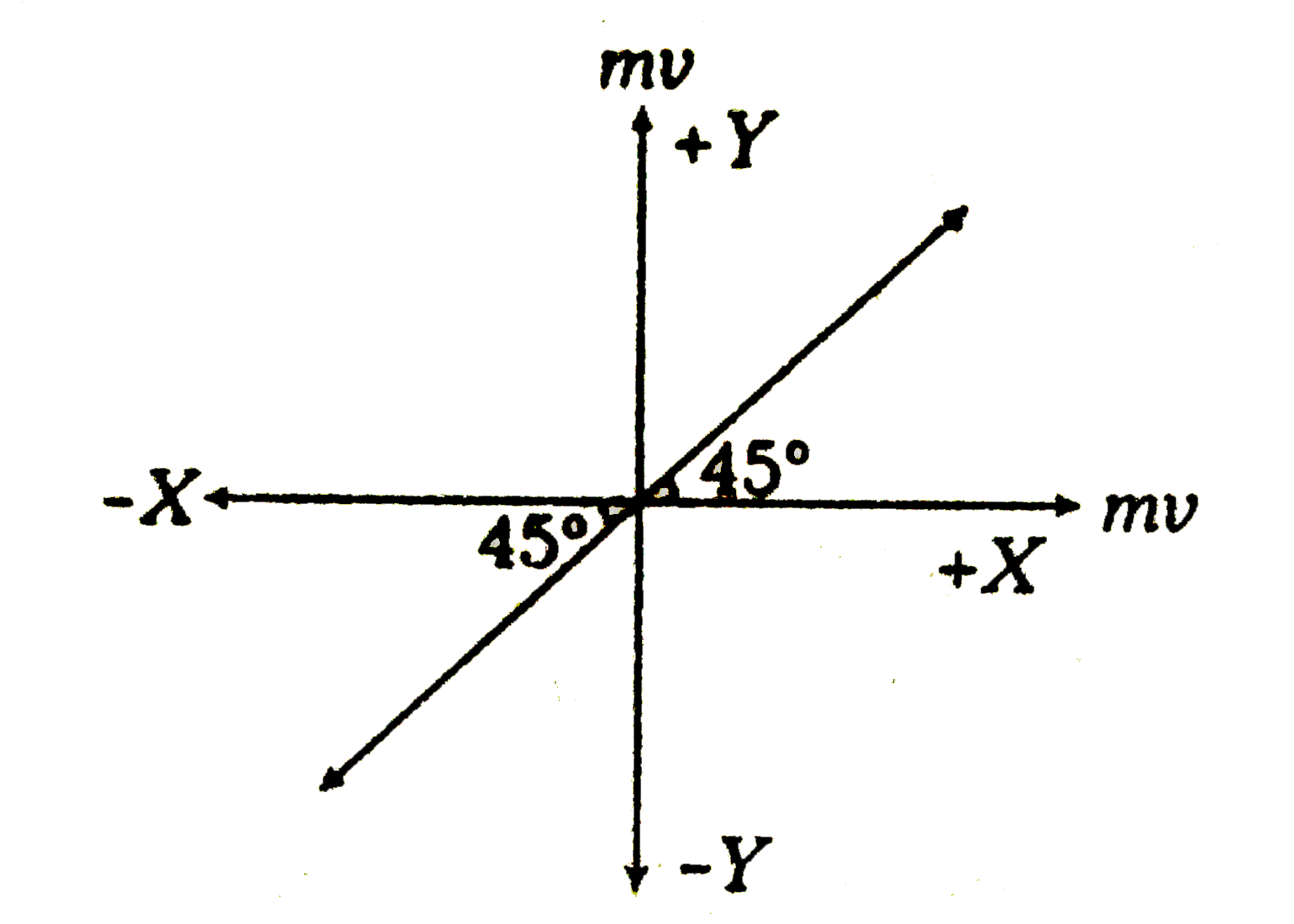
$\sqrt{m v}$ = Resultant momentum of two small masses
$\sqrt{2} (m v) = (2 m) \times v^{'} = \frac{v}{\sqrt{2}}$
So, total kinetic energy generated by the explosion
$= \frac{1}{2} m^{2} + \frac{1}{2} m v^{2} + \frac{1}{2} (2 m) v^{' 2}$
$- m v^{2} + m \times {(\frac{v}{\sqrt{2}})}^{2}$
$= m v^{2} + \frac{m v^{2}}{2} = \frac{3}{2} m v^{2}$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A body of mass (4m) is laying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each mass (m) move perpedicular to each other with equal speeds (v). Total kinetic energy generated due to explosion is
A $m v^{2}$
B $\frac{3}{2} m v^{2}$
C $2 m v^{2}$
D $4 m v^{2}$
Question 2 - Select One
A body of mass (4m) is lying in x-y plane at rest. It suddenly explodes into three pieces. Two pieces, each of mass (m) move perpendicular to each other with equal speeds (v). The total kinetic energy generated due to explosion is
A $m v^{2}$
B $\frac{3}{2} m v^{2}$
C $2 m v^{2}$
D $4 m v^{2}$
Question 3 - Select One
The objects at rest suddenly explodes into three parts with the mass ratio 2:1:1. The parts of equal masses moves at right angles to each other with equal speeds. The speed of the third part after the explosion will be
A2v
B $\frac{v}{\sqrt{2}}$
C $\frac{v}{2}$
D $\sqrt{2} v$

DC PANDEY-CENTRE OF MASS-Medical entrances gallery

Home
Ask Doubt
Profile