A particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
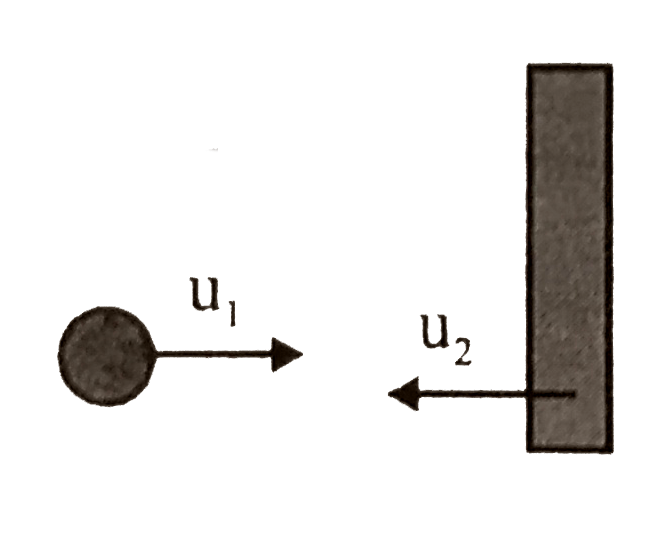
Velocity of approach
uapproch=(u1+u2)
Let the velocity of the particle just after the collision be →v1.
The velocity of separation,
vseperation=(v1−v2)
Since, according to Newton's experimental law
e=v1−v2u1+u2
As there is no loss of energy, collision is elastic
Putting the value of e=1, we obtain
v1−v2(u1+u2)=1 or u1+u2=v1−v2
or v1=u1+u2+v2
Putting u1=20m/s,u2=5m/s and v2=u2' since the wall being very heavy (infinite mass).
moves with constant velocity, we obtain
v1=v0+2v=20+2(5)=30m/sec.
Solving (i)&(ii), we obtain v1=127m/s,v2=267m/s
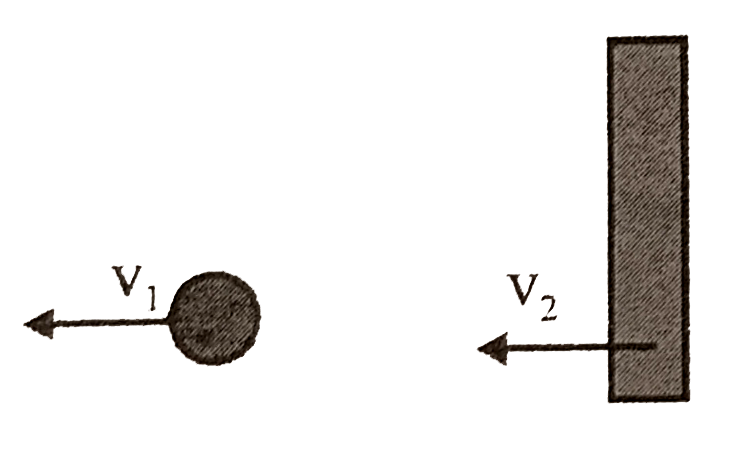
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:Solved Examples
Explore 15 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBook:BANSALChapter:CENTRE OF MASS & MOMENTUM CONSERVATIONExercise:Practice Exercise
Explore 20 Videos
- GRAVITATIONBook:BANSALChapter:GRAVITATIONExercise:EXERCISE -4 Section - B
Explore 6 Videos
Similar Questions
A particle of mass m moving on a smooth surface with velocity 10m/s strikes another particle of mass 2m moving with 5m/s in the same direction . If the collision is elastic and head - on , find velocities of particles after the collision.
View SolutionA particle of mass m moving with velocity v0 collides with sphere of same mass at rest , as shown. If the surface of contact is smooth and the collision is elastic, find the velocities of particle and sphere after the collision.

View Solution
Knowledge Check
A ball is moving with velocity 2m/s towards a heavy wall moving towards the ball with speed 1m/s as shown in figure. Assuming collision to be elastic, find the velocity of ball immediately after the collision.
 Av=4m/sBv=3m/sCv=0m/sDv=1m/s
Av=4m/sBv=3m/sCv=0m/sDv=1m/sA particle is moving with velocity 5 m/s towards cast and its velocity changes to 5 m/s north in 10 s, find the acceleration .
A√2 North- WestB1√2 North - WestC1√2 North - EastD√2 North -EastA particle is moving with velocity 5 m/s towards cast and its velocity changes to 5 m/s north in 10 s, find the acceleration .
A√2 N-WB1√2 N-WC1√2 N-ED√2N−E
A particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View SolutionA particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionA particle of mass m moving with velocity 2v collides with another particle of mass 3m moving with velocity v in the same direction.If it is perfect inelastic collision,the loss of kinetic energy of the system is
View SolutionA particle of mass m moving with velocity u1 collide elastically with another particle of same mass moving with velocity u2 in the same direction. After collision their speeds are v1 and v2 respectively then
(A) u1+v1=v2+u2, (B) u1−v1=v2+u2
View Solution