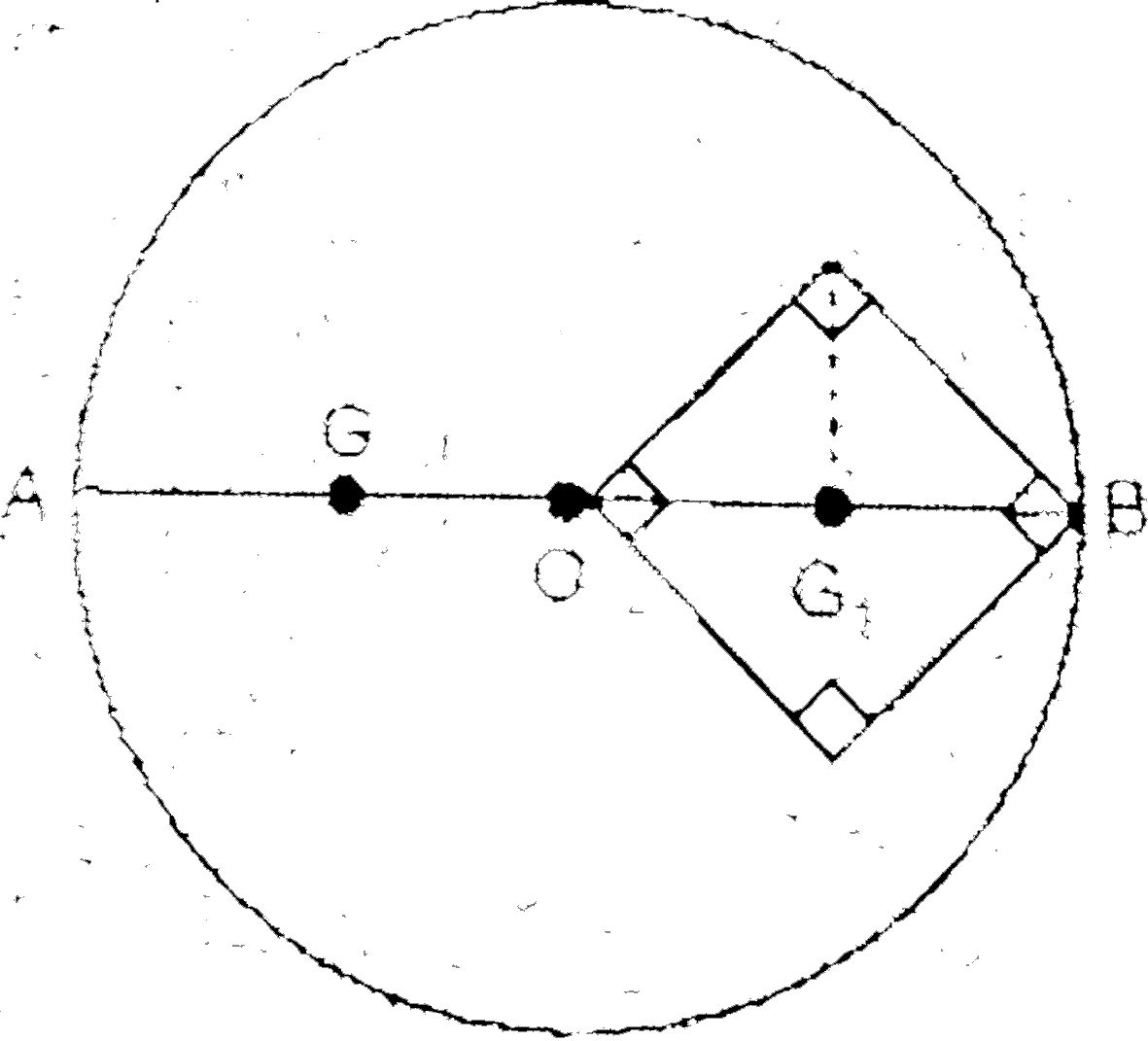
A square hole is punched out of a circular lamina, the diagonal of the square being the radius of the circle. If 'a' be the diameter of the sircle, find the distance of centre of mass of the remainder from the centre of the circle.
To find the distance of the center of mass of the remaining part of the circular lamina after a square hole is punched out, we can follow these steps:
Step 1: Define the Problem
We have a circular lamina with a diameter a. The radius r of the circle is given by:
r=a2
A square hole is punched out from this circular lamina, and the diagonal of the square is equal to the radius of the circle.
Step 2: Determine the Side Length of the Square
Let the side length of the square be s. The relationship between the side length and the diagonal of the square is given by:
s√2=r
Substituting r=a2:
s√2=a2
From this, we can solve for s:
s=a2√2=a√24
Step 3: Calculate the Areas
The area of the circular lamina Ac is:
Ac=πr2=π(a2)2=πa24
The area of the square As is:
As=s2=(a√24)2=a28
Step 4: Calculate the Masses
Assuming uniform density ρ:
- Mass of the circular lamina Mc:
Mc=ρAc=ρ⋅πa24
- Mass of the square Ms:
Ms=ρAs=ρ⋅a28
Step 5: Find the Center of Mass of the Remaining Lamina
The center of mass of the circular lamina is at the origin (0, 0). The center of mass of the square (which is removed) can be calculated as it is located at the center of the square:
Center of mass of square=(0,0)
Step 6: Use the Formula for the Center of Mass of the Remaining Lamina
The center of mass xcm of the remaining part can be found using the formula:
xcm=Mc⋅xc−Ms⋅xsMc−Ms
Since both centers of mass are at the origin, this simplifies to:
xcm=Mc⋅0−Ms⋅0Mc−Ms=0
Step 7: Conclusion
The distance of the center of mass of the remaining part from the center of the circle is:
Distance=0
We have a circular lamina with a diameter a. The radius r of the circle is given by:
r=a2
A square hole is punched out from this circular lamina, and the diagonal of the square is equal to the radius of the circle.
Let the side length of the square be s. The relationship between the side length and the diagonal of the square is given by:
s√2=r
Substituting r=a2:
s√2=a2
From this, we can solve for s:
s=a2√2=a√24
The area of the circular lamina Ac is:
Ac=πr2=π(a2)2=πa24
The area of the square As is:
As=s2=(a√24)2=a28
Assuming uniform density ρ:
- Mass of the circular lamina Mc:
Mc=ρAc=ρ⋅πa24
- Mass of the square Ms:
Ms=ρAs=ρ⋅a28
The center of mass of the circular lamina is at the origin (0, 0). The center of mass of the square (which is removed) can be calculated as it is located at the center of the square:
Center of mass of square=(0,0)
The center of mass xcm of the remaining part can be found using the formula:
xcm=Mc⋅xc−Ms⋅xsMc−Ms
Since both centers of mass are at the origin, this simplifies to:
xcm=Mc⋅0−Ms⋅0Mc−Ms=0
The distance of the center of mass of the remaining part from the center of the circle is:
Distance=0
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
23 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
A square hole is punched out of a circular lamina, the diagonal of the square being the radius of the circle. If 'a' br the diameter of the circle, find the distance of C.G. of the reamainder form the centre of the circle.
View SolutionThe length of a chord of a circle is equal to the radius of the circle. Compare the distance of the chord from the centre with the radius of the circle.
View Solution
Knowledge Check
A square hole is punched out of a circular lamina of diameter a. The diagonal of the square is equal to the radius of the circle and one of the corners is at the centre of the circle . The distance of the C.G. of the remainder from the centre of circle is
Aa8π+4Ba8π−4Ca5π−4Da5π+4A square hole is punched out of a circular lamina of diameter 4 cms., the diagonal of the square being a radius of the circle. Centroid of the remainder from the centre of the circle is at a distance
A12π+1B12π−1C1π+1D1π−1From a circle of radius a, an isosceles right angles triangle with the hypotenuse as the diameter of the circle is removed. The distance of the centre of mass of the remaining portion from the centre of the circle is
A3(π−1)aB(π−1)a6Ca3(π−1)Da3(π+1)
Find out the position of centre of mass of the uniform lamina as shown in figure.

View SolutionA square ABCD is inscribed in a circle of radius r. Find the area of the square.
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionIf the diameter of a circle is equal to the diagonal of a square, then the ratio of their areas is ________.
View Solution