A glass ball collides with a smooth horizontal surface (xz plane) with a velocity V=ai−bj. If the coefficient of restitution of collision be e, the velocity of the ball just after the collision will be
Collision takes place along the normal. Therefore the magnitude normal component (vy) of the velocity of the glass ball is changed tovy'=e vy just after the collision whereas the horizontal component (vx) of its velocity remains constant due to the absence of any horisontal force.
⇒ The velocity of the ball just after the impact
=→v=→vx+→vy
⇒ →v'=v'xˆi+v'yˆj
where, v'x=a & v'y=eb
⇒ →v'=aˆi+ebˆj
Therefore the magnitud of the velocity →v'=|→v'|=√a2+e2b2 and the direction is given as
θ=tan−1(vx'vy')=tan−1(aeb) to the normal (vertical)
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - Practice Exercise
20 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-1 [SINGLE CORRECT CHOICE TYPE]
23 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View Solution
Knowledge Check
A ball of mass m is projected with a velocity 'u' at angle θ with the horizontal. It collides with a smooth box of mass 'M' at its highest position. If the co-efficient of restitution is 'e'.
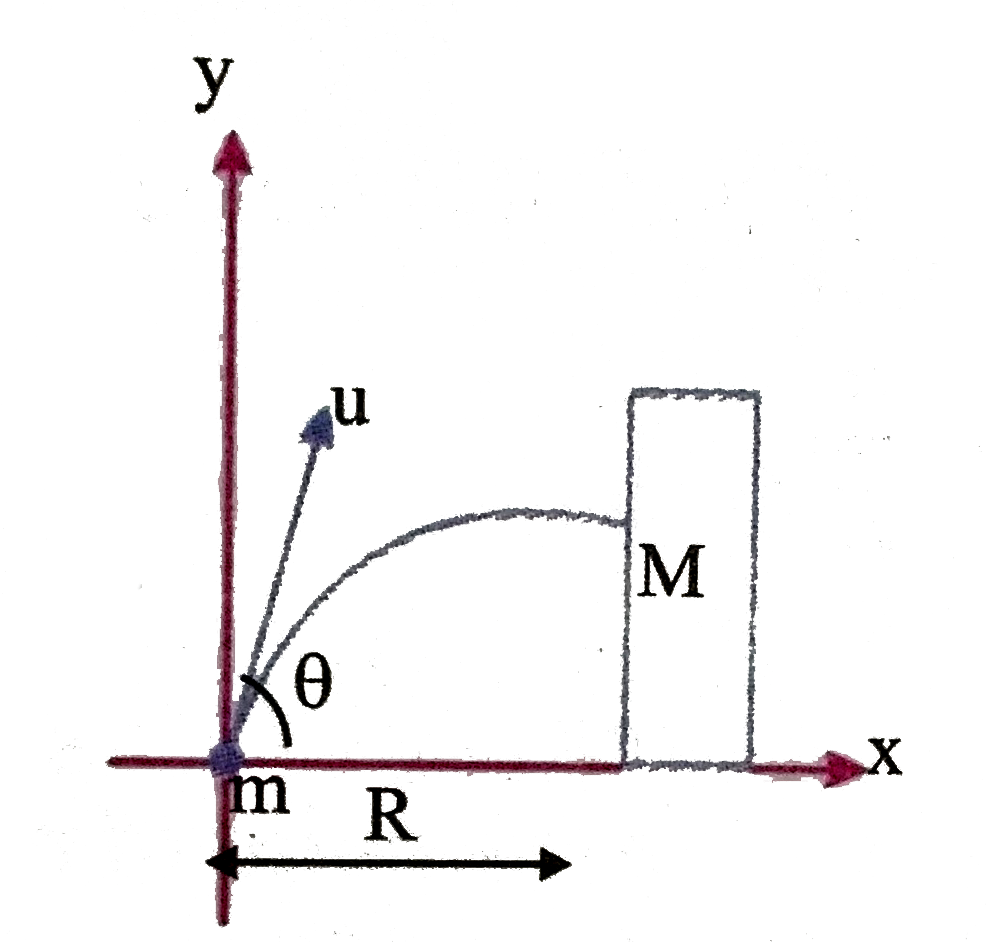
FInd the velocity of the ball after collisionA(m−eMM+m)ucosθB(M−emM+m)ucosθC(m+eMM+m)usinθD(m−eMM+m)usinθA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
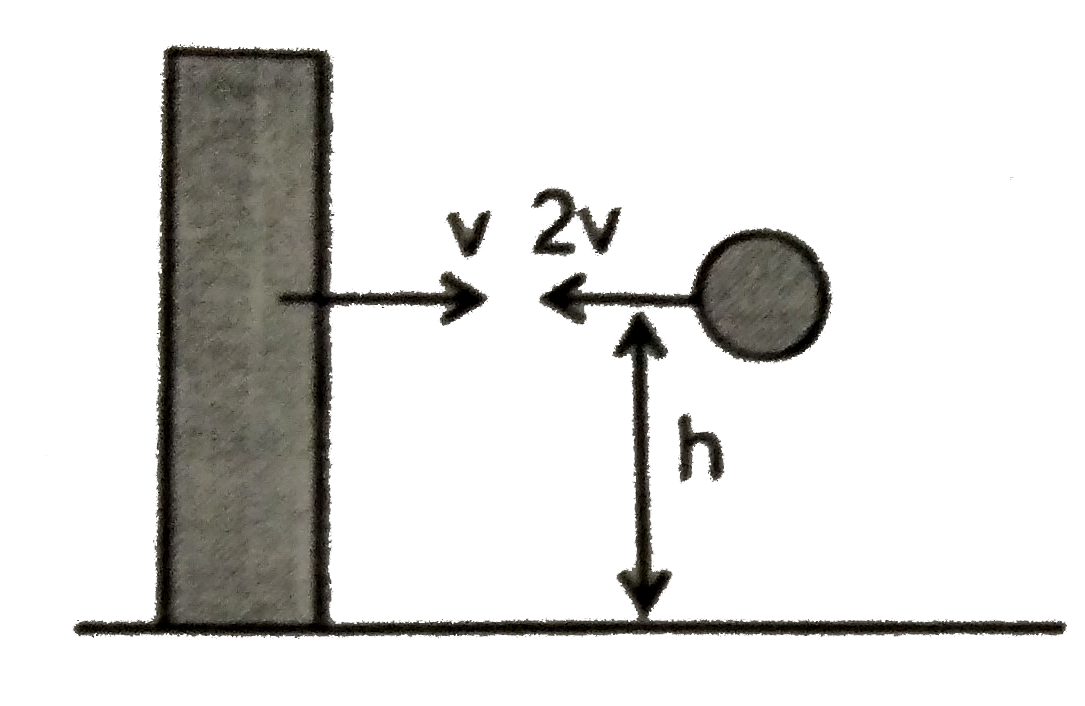 Av√2hgB2v√2hgC3v√2hgD4v√2hg
Av√2hgB2v√2hgC3v√2hgD4v√2hgAB is an L shaped obstacle fixed on a horizontal smooth table. A ball strikes it at A, gets deflected and restrikes it at B. if the velocity vector before collision is →v and coefficient of restitution of each collision is 'e', then the velocity of ball after its second collision at B is
 Ae2→vB−e2→vC−e→vDdata insufficient
Ae2→vB−e2→vC−e→vDdata insufficient
A small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
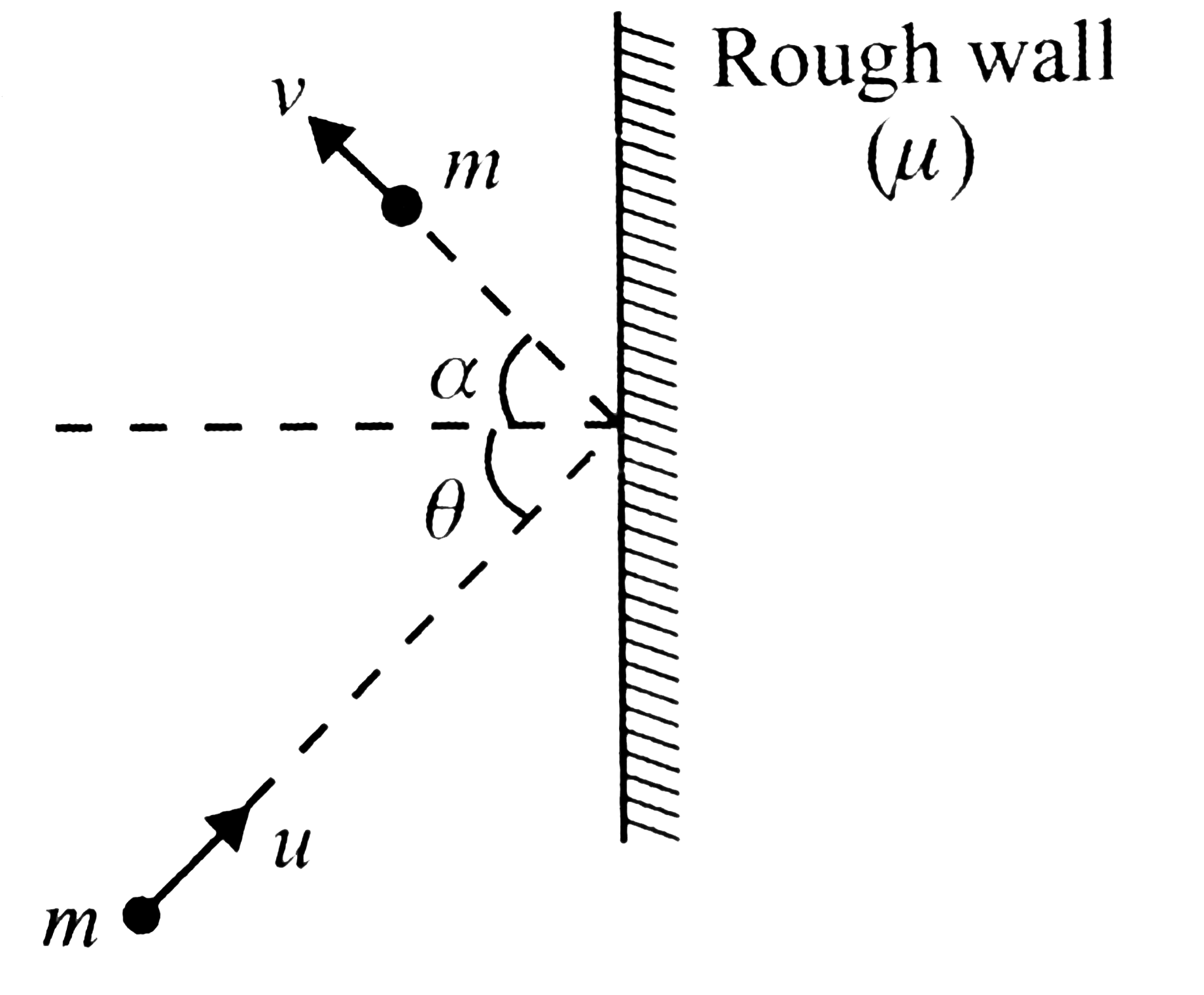
View SolutionA ball P is moving with a certain velocity , collides head-on with another ball Q of same mass is rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionA ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionBall 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?
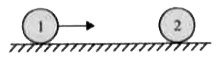
View Solution