Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
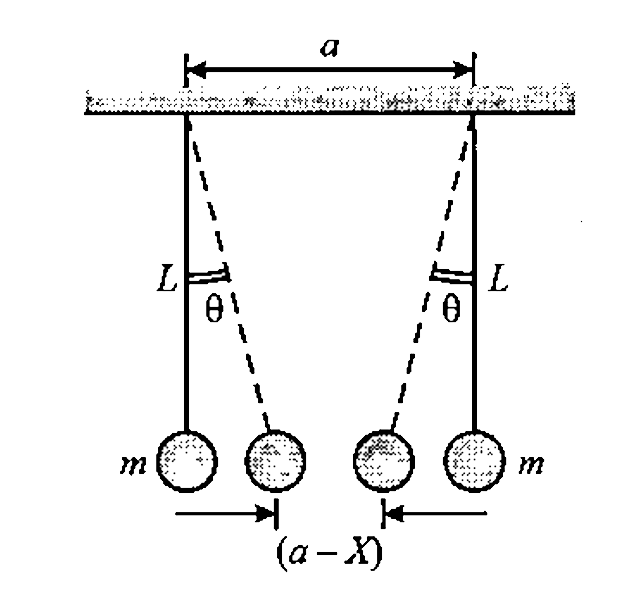
tan−1(a−X)gmG
tan−1mG(a−X)2g
tan−1(a−X)2gmG
tan−1(a2−X2)gmG
The correct Answer is:B
Step by step video, text & image solution for Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle theta that the threads will make with the vertical due to attraction between the balls is : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Advance MCQs
Explore 17 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Unsolved Numerical
Explore 94 Videos
- GRAVITATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:GRAVITATIONExercise:Concetual MCQ
Explore 39 Videos
- FLUID MECHANICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:FLUID MECHANICSExercise:Unsolved Numerical Problems
Explore 86 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
Similar Questions
Two balls of mass m each are hung side by side by side by two long threads of equal length l. If the distance between upper ends is r, show that the distance r' between the centres of the ball is given by gr'2(r−r')=2lGm
View SolutionTwo small spheres, each of mass 0.1 gm and carrying same charge 10−9C are suspended by threads of equal length from the same point. If the distance between the centres of the sphere is 3 cm, then find out the angle made by the thread with the vertical. (g=10m/s2) & tan−1(1100)=0.6º
View Solution
Knowledge Check
Two metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is l. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
Atan−1(Gmgl2Btan−1(GmgL2Ctan−1(Gmgl)Dtan−1(GmgL)Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure (R<<L). The angle, θ which mass m2 makes with the vertical is approximately -
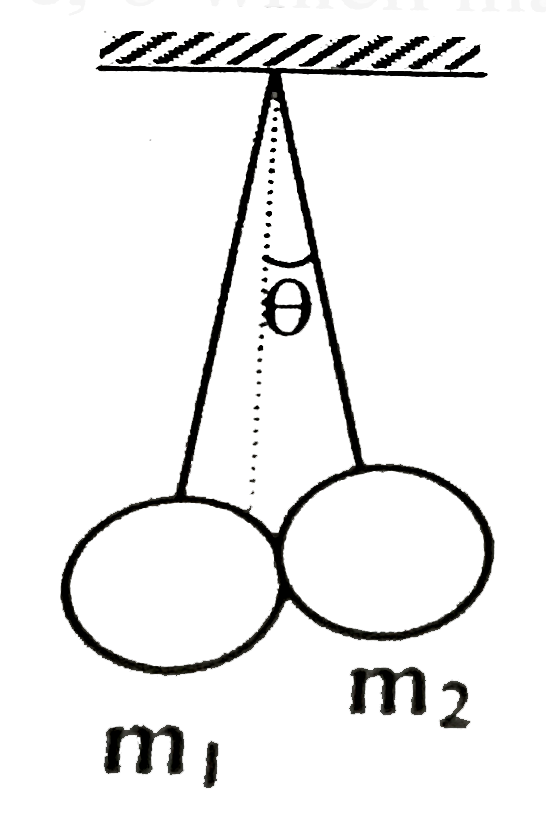 Am1R(m1+m2)LB2m1R(m1+m2)LC2m2R(m1+m2)LDm2R(m1+m2)L
Am1R(m1+m2)LB2m1R(m1+m2)LC2m2R(m1+m2)LDm2R(m1+m2)LA small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg.
Two idential pith balls , each of mass m and charge +q. are suspended from a point with threads of length l each. If in equiilbrium state θ be the angle which each thread makes with vertical in equilibrium , find value of charge on each ball.
View SolutionTwo identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionTwo small balls, each having charge q, are suspended by two insulating threads of equal length L fron a hook in an elevator. The elevator is freely falling. Calculate the angle etween the two threads and tension in each thread.
View SolutionTwo identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle 'θ' with the vertical ?
View SolutionTwo small metal balls of different mass m1 and m2 are connected by strings of equal length to a fixed point. When the balls are given equal charges, the angles that the two strings make with the vertical are 30∘ and 60∘, respectively. The ratio m1/m2 is close to -
View Solution

