A body which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth. Find out its velocity on reaching the surface of earth. Take g= acceleration due to gravity on the surface of the Earth.
√43gR
√23gR
43gR
2gR
The correct Answer is:A
Step by step video, text & image solution for A body which is initially at rest at a height R above the surface of the earth of radius R, falls freely towards the earth. Find out its velocity on reaching the surface of earth. Take g= acceleration due to gravity on the surface of the Earth. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Advance MCQs
17 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Unsolved Numerical
94 Videos
- GRAVITATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GRAVITATIONEXERCISE - Concetual MCQ
39 Videos
- FLUID MECHANICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - FLUID MECHANICSEXERCISE - Unsolved Numerical Problems
86 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
Similar Questions
A body which is initially at rest at a height h=6400km above the surface of the earth of radius R(6400km), falls freely towards the earth. If its velocity on reaching the surface of earth is 2N×103ms, then calculate N. (Take g= acceleration due to gravity on the surface of the earth =10m(s)2 )
View SolutionIf R is the radius of the earth and g the acceleration due to gravity on the earth's surface, the mean density of the earth is
View Solution
Knowledge Check
A geostationary satellite is at a height h above the surface of earth. If earth radius is R-
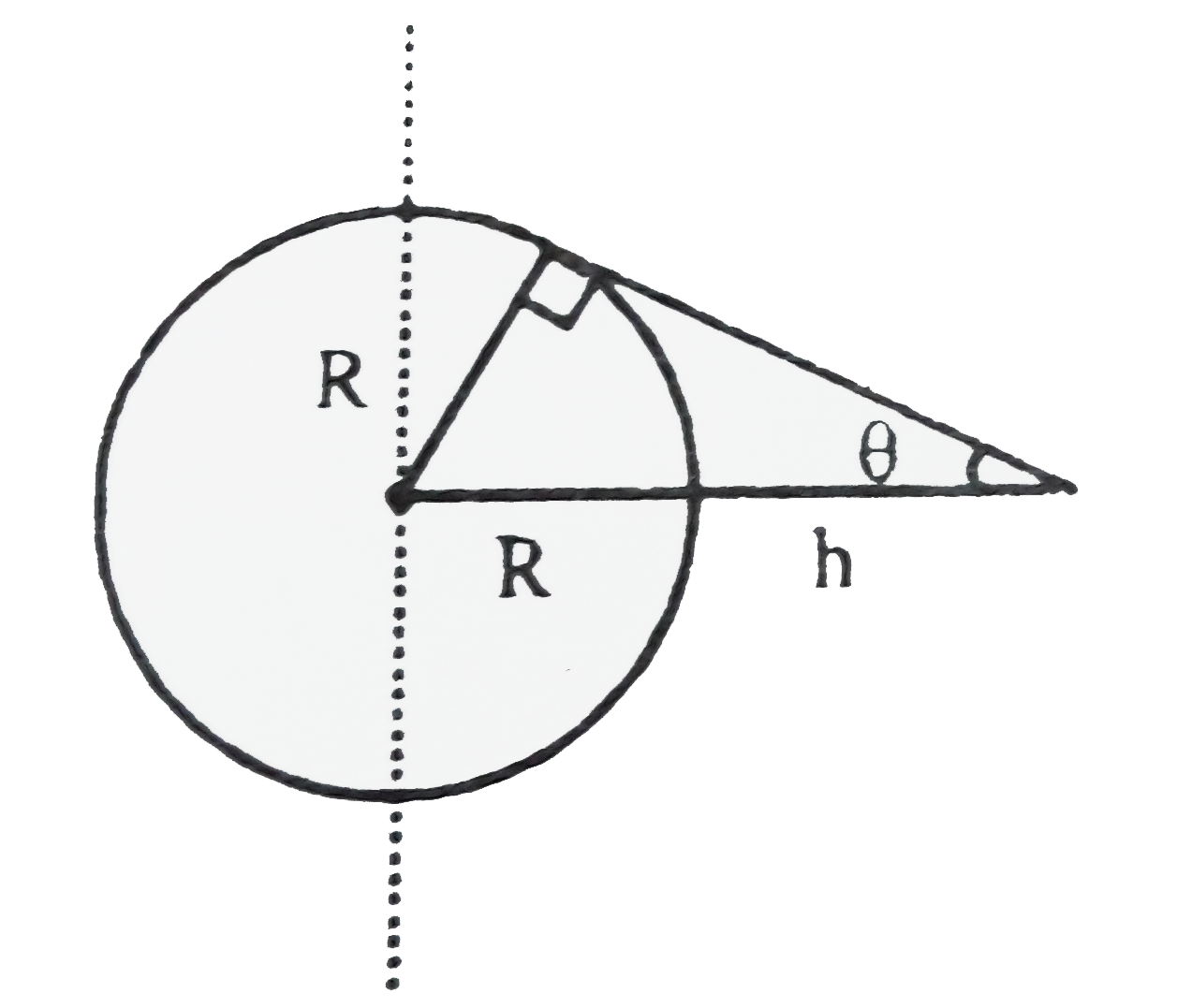 AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)
AThe minimum colatitude on earth upto which the satellite can be used for communication is sin−1(R/R+h)BThe maximum colatitudes on earth upto which the satellite can be used for communication is sin−1(R/R+h)CThe area on earth escaped from this satellite is given as (2πR2(1+sinθ))DThe area on earth escaped from this satellite is given as (2πR2(1+cosθ)A small body of mass m falls to the earth from infintie distance away. What will be its velocity or reaching the earth? (Radius of the earth = R, acceleration due to gravity on the surface of the earth is g) :-
AgRB2gRC√gRD√2gRWhat will be the acceleration due to gravity at height h if h gt gt R . Where R is radius of earth and g is acceleration due to gravity on the surface of earth
Ag(1+hR)2Bg(1−2hR)Cg(1−hR)2Dg(1−hR)
The acceleration of a body due to the attraction of the earth (radius R) at a distance 2R form the surface of the earth is (g=acceleration due to gravity at the surface of the earth)
View SolutionGiven, acceleration due to gravity on surface of earth is g. if g' is acceleration due to gravity at a height h above the surface of earth, then
View SolutionIf the radius of the earth is 6400 km, the height above the surface of the earth where the value of acceleration due to gravity will be 4% of its value on the surface of the earth is
View SolutionIf R is the radius of the earth and g the acceleration due to gravity on the earth’s surface, the mean density of the earth is
View SolutionWhat will be the acceleration due to gravity at height h<<R . Where R is radius of earth and g is acceleration to gravity on the surface earth
View Solution
