Two small spheres, each of mass 0.1 gm and carrying same charge 10−9C are suspended by threads of equal length from the same point. If the distance between the centres of the sphere is 3 cm, then find out the angle made by the thread with the vertical. (g=10m/s2) & tan−1(1100)=0.6º
The correct Answer is:tan−1(1/100)=0.6º
To solve the problem, we will follow these steps:
Step 1: Understand the system
We have two small spheres, each with a mass of 0.1 g (which is 0.1 x 10^-3 kg) and each carrying a charge of 10−9C. They are suspended by threads of equal length from the same point, and the distance between the centers of the spheres is 3 cm (which is 0.03 m).
Step 2: Convert mass to kg
Convert the mass of the spheres from grams to kilograms:
m=0.1g=0.1×10−3kg=1×10−4kg
Step 3: Calculate the electrostatic force between the spheres
Using Coulomb's law, the electrostatic force Fe between the two charges is given by:
Fe=kq1q2r2
Where:
- k=9×109N m2/C2 (Coulomb's constant)
- q1=q2=10−9C
- r=0.03m
Substituting the values:
Fe=9×109(10−9)2(0.03)2
Fe=9×10910−180.0009=9×109×1.1111×10−15=10−5N
Step 4: Analyze forces acting on the spheres
Each sphere experiences three forces:
1. The gravitational force Fg=mg acting downwards.
2. The tension T in the thread acting along the thread.
3. The electrostatic force Fe acting horizontally (repulsive force).
Step 5: Calculate the gravitational force
Fg=mg=(1×10−4kg)(10m/s2)=1×10−3N
Step 6: Set up the equations of motion
Using the equilibrium of forces:
- Vertically: Tcosθ=Fg
- Horizontally: Tsinθ=Fe
Dividing these two equations:
TsinθTcosθ=FeFg
tanθ=FeFg
Step 7: Substitute the values
Substituting the values we calculated:
tanθ=10−51×10−3=0.01
Step 8: Calculate the angle
Now, using the inverse tangent function:
θ=tan−1(0.01)
Using the given hint:
tan−1(1/100)≈0.6∘
Thus, the angle made by the thread with the vertical is approximately 0.6∘.
Final Answer
The angle made by the thread with the vertical is approximately 0.6∘.
---
We have two small spheres, each with a mass of 0.1 g (which is 0.1 x 10^-3 kg) and each carrying a charge of 10−9C. They are suspended by threads of equal length from the same point, and the distance between the centers of the spheres is 3 cm (which is 0.03 m).
Convert the mass of the spheres from grams to kilograms:
m=0.1g=0.1×10−3kg=1×10−4kg
Using Coulomb's law, the electrostatic force Fe between the two charges is given by:
Fe=kq1q2r2
Where:
- k=9×109N m2/C2 (Coulomb's constant)
- q1=q2=10−9C
- r=0.03m
Fe=9×109(10−9)2(0.03)2
Fe=9×10910−180.0009=9×109×1.1111×10−15=10−5N
Each sphere experiences three forces:
1. The gravitational force Fg=mg acting downwards.
2. The tension T in the thread acting along the thread.
3. The electrostatic force Fe acting horizontally (repulsive force).
Fg=mg=(1×10−4kg)(10m/s2)=1×10−3N
Using the equilibrium of forces:
- Vertically: Tcosθ=Fg
- Horizontally: Tsinθ=Fe
TsinθTcosθ=FeFg
tanθ=FeFg
Substituting the values we calculated:
tanθ=10−51×10−3=0.01
Now, using the inverse tangent function:
θ=tan−1(0.01)
tan−1(1/100)≈0.6∘
Thus, the angle made by the thread with the vertical is approximately 0.6∘.
The angle made by the thread with the vertical is approximately 0.6∘.
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Exercise-1 Section (B)
Explore 12 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Exercise-1 Section (C)
Explore 14 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:Problems
Explore 22 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCEChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
Two small identical balls P and Q, each of mass 0.866 g, carry identical charges and are suspended by two threads of equal length 50 cm each from the same point. At equilibrium, they are separated by a distance of 50 cm. Find the charge on each ball (in nearest integer in nC).
View Solution2 small spheres each of mass m and carrying +q coulomb, are suspended by massles insulating threads, each of length l. Prove that q2=(4mgl2sin2θtanθ)4πε0, where θ is angle made of strings with the vertical at equilibrium.
View Solution
Knowledge Check
Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
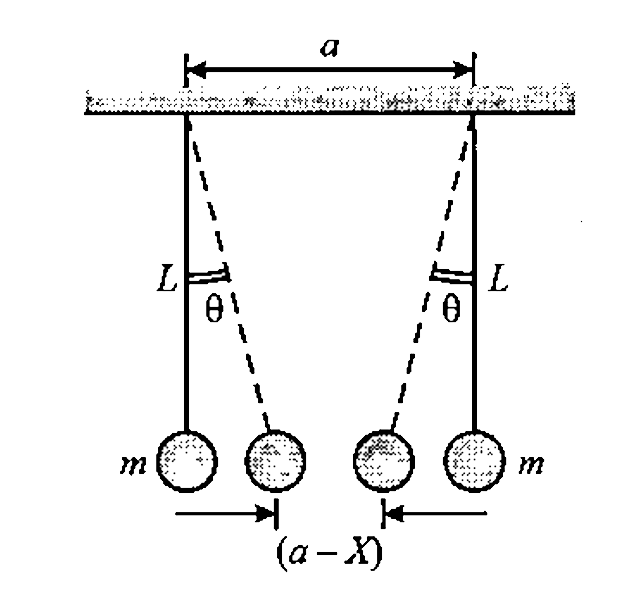 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmGAn isolated conducting sphere of radius 0.1m placed in vacuum carries a positive charge of 0.1μC. Find the electric intensity at a point at a distance 0.2 m from the centre of the sphere.
A2.25×102N/CB2.25×104N/CC2.52×102N/CD2.52×104N/C
Two small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
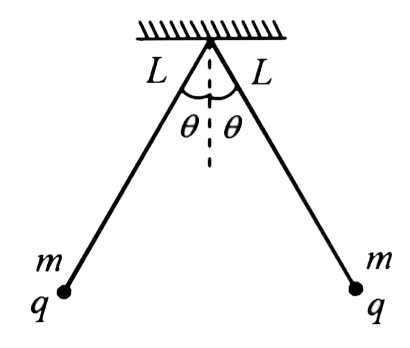
View SolutionA sphere of mass 25 kg attracts another sphere of mass 24kg with a force of 0.1 milligram weight. if distance between the centres of two sphere is 20 cm, what is the value of G ?
View SolutionTwo identical spheres of mass m and charge q are suspended from a common point by two threads of the same length l and it is found that threads make an angle θ with the vertical when the spheres are in equilibrium . Calculate the value of q.
View SolutionTwo small spheres each of mass 10 mg are suspended from a point by threads 0.5 m long. They are equally charged and repel each other to a distance of 0.20 m. The charge on each of the sphere is a21×10−8C. The value of 'a' will be _______.
[Given g=10ms−2]
View SolutionTwo balls of same mass and carrying equal charge are hung by threads of length l from a fixed support, At electrostatic equilibrium.assuming that angles made by each thread is small,the separation, x between the balls is proportional to:
View SolutionTwo small spheres each of mass 'm' kg and charge q coulomb are suspended from a point by insulating threads each of 1 metre length, but of negliglible mass. If θ is the angle which each string makes with the verticle vertical when equilbrium has been reached, show that
q2=4mgl2sin2θtanθ(4π∈0)
View Solution

