Question

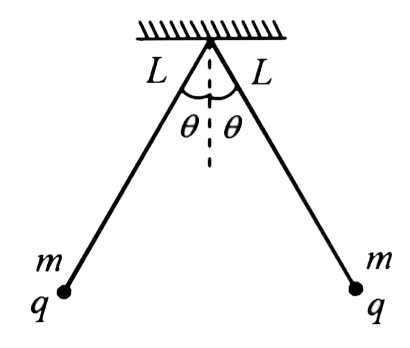
Two small spheres each of mass 'm' kg and charge q coulomb are suspended from a point by insulating threads each of 1 metre length, but of negliglible mass. If ${\displaystyle \theta }$ is the angle which each string makes with the verticle vertical when equilbrium has been reached, show that
${\displaystyle q^2=4mg{l}^2{\sin }^2\theta \tan \theta \left(4\pi {\in }_0\right)}$

Answer

`q^(2) = 4 mg l^(2) sin^(2) tan theta. 4pi in_(0)`

Explanation

To solve the problem, we need to analyze the forces acting on each sphere when they are in equilibrium. Here’s a step-by-step solution:

Step 1: Understand the Setup
We have two small spheres, each with mass \( m \) and charge \( q \), suspended by insulating threads of length \( l \). When in equilibrium, each thread makes an angle \( \theta \) with the vertical.

Step 2: Identify Forces Acting on Each Sphere
Each sphere experiences:
- Gravitational force \( F_g = mg \) acting downwards.
- Tension \( T \) in the thread acting along the thread.
- Electrostatic force \( F_e \) due to the repulsion between the two charged spheres.

Step 3: Resolve the Tension Force
The tension \( T \) can be resolved into two components:
- Vertical component: \( T \cos \theta \)
- Horizontal component: \( T \sin \theta \)

Step 4: Apply Equilibrium Conditions
In equilibrium:
1. The vertical forces must balance:
\( T \cos \theta = mg \tag{1} \)
2. The horizontal forces must balance (the electrostatic force equals the horizontal component of tension):
\( T \sin \theta = F_e \tag{2} \)

Step 5: Calculate the Electrostatic Force
The electrostatic force \( F_e \) between the two charges is given by Coulomb's law:
\( F_e = \frac{k q^2}{r^2} \)
where \( k = \frac{1}{4 \pi \epsilon_0} \) and \( r \) is the distance between the two spheres.

Step 6: Determine the Distance \( r \)
Using geometry, the distance \( r \) between the two spheres can be expressed as:
\( r = 2l \sin \theta \)

Step 7: Substitute \( r \) into the Electrostatic Force Equation
Substituting \( r \) into the expression for \( F_e \):
\( F_e = \frac{k q^2}{(2l \sin \theta)^2} = \frac{k q^2}{4l^2 \sin^2 \theta} \)

Step 8: Substitute \( F_e \) into Equation (2)
From Equation (2):
\( T \sin \theta = \frac{k q^2}{4l^2 \sin^2 \theta} \)

Step 9: Substitute \( T \) from Equation (1)
From Equation (1), we can express \( T \):
\( T = \frac{mg}{\cos \theta} \)
Substituting this into the equation gives:
\( \frac{mg}{\cos \theta} \sin \theta = \frac{k q^2}{4l^2 \sin^2 \theta} \)

Step 10: Rearranging the Equation
Now, rearranging the equation:
\( mg \tan \theta = \frac{k q^2}{4l^2 \sin^2 \theta} \)
Multiplying both sides by \( 4l^2 \sin^2 \theta \):
\( 4mgl^2 \sin^2 \theta \tan \theta = k q^2 \)

Step 11: Substitute \( k \)
Substituting \( k = \frac{1}{4 \pi \epsilon_0} \):
\( 4mgl^2 \sin^2 \theta \tan \theta = \frac{1}{4 \pi \epsilon_0} q^2 \)

Step 12: Final Rearrangement
Rearranging gives:
\( q^2 = 4mgl^2 \sin^2 \theta \tan \theta (4 \pi \epsilon_0) \)

Conclusion
Thus, we have shown that:
\( q^2 = 4mg l^2 \sin^2 \theta \tan \theta (4 \pi \epsilon_0) \)