Two balls of mass m each are hung side by side by side by two long threads of equal length l. If the distance between upper ends is r, show that the distance r' between the centres of the ball is given by gr'2(r−r')=2lGm
The situation is shown in figure

Following force act on each ball
(i) Weight of the ball m g in downward direction
(ii) Tension in thread T along string
(iii) Force of gravitation attraction towards each other
F=Gmmr'2
Here for equilibrium of balls we have
Tsinθ=Gm2r'2 ....(i)
Tcosθ=mg .....(ii)
Dividing equation (i) and (ii), we get
or tanθ=Gm2mgr'2 .....(iii)
In ΔACP tan θ=r−r'2l .....(iv)
From equation (iii) and (iv)
r−r'2l=Gm2mgr'2
gr'2(r−r')=2lGm
For partical consideration, it is viable to assume that the two masses. will be attracted by very small distance as gravitational force acting between then will be very less. Hence, the balls will be at almost the same horizontal level as before or θ will be very small.
Topper's Solved these Questions
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Solved Example
8 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - Practice Exercise
18 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)
8 Videos
- HEAT TRANSFERBOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise
89 Videos
Similar Questions
Knowledge Check
Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
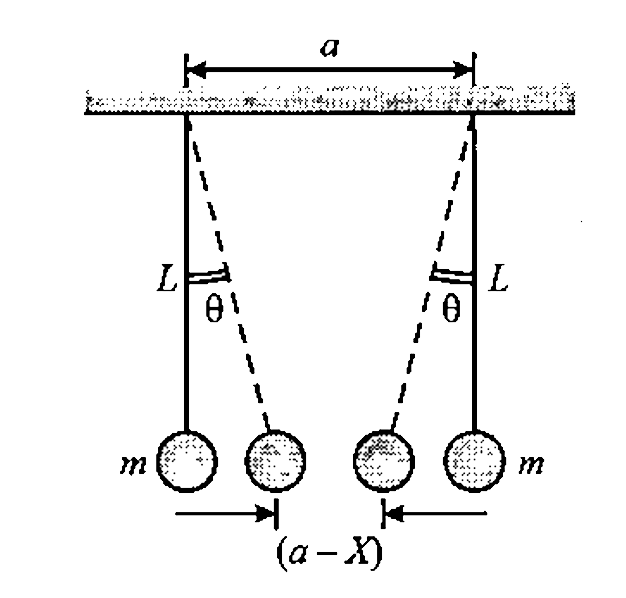 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmGTwo metallic balls of mass m are suspended by two strings of length L. The distance between upper ends is l. The angle at which the string will be inclined with vertical due to attraction is (m<<M where M is the mass of Earth)
Atan−1(Gmgl2Btan−1(GmgL2Ctan−1(Gmgl)Dtan−1(GmgL)R and r are the radius of two circles (R>r). If the distance between the centre of the two circles be d, then length of common tangent of two circles is
A√d2−(R−r)2B√(R−r)2−d2C√R2−d2D√r2−d2
Three identical spheres each of radius R are placed touching side by side along X axis so that the centre of the first sphere is at the origin. Now the sphere at the extreme end is removed. The shift in the centre of mass is (A) R (B) 2R (C) R 2 (D) 3R
View SolutionA solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View SolutionR and r are the radii of two circles (R > r). If the distance between the centres of the two circles be d, then length of common tangent of two circles is
View SolutionIF two circles of radii r1 and r2 (r2>r1) touch internally , then the distance between their centres will be
View SolutionTwo sides of a triangle are the roots of the equation x2−5x+6=0. If the angle between the sides is π3, then r.R=
View Solution