Two bars connected by a weightless spring of stiffness ϰ and length (in the non-deformed state) l0 rest on a horizontal plane. A constant horizontal force F starts acting on one of the bars as shown in figure. Find the maximum and minimum distances between the bars during the subsequent motion of the system, if the masses of the bars are:
(a) equal:
(b) equal to m1 and m2, and the force F is applied to the bar of mass m2.

The correct Answer is:[lmaxl0+F/k,lmin=l0,lmax=l0+2m1F/k(m1+m2)]
Step by step video, text & image solution for Two bars connected by a weightless spring of stiffness ϰ and length (in the non-deformed state) l_0 rest on a horizontal plane. A constant horizontal force F starts acting on one of the bars as shown in figure. Find the maximum and minimum distances between the bars during the subsequent motion of the system, if the masses of the bars are: (a) equal: (b) equal to m_1 and m_2, and the force F is applied to the bar of mass m_2. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:exercise 1.3
Explore 3 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:LINEAR MOMENTUM & ITS CONSERVATIONExercise:Advance McQ
Explore 20 Videos
- KINEMATICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:KINEMATICSExercise:Unsolved Numerical Pro.
Explore 83 Videos
- NEWTONS LAWS OF MOTIONBook:PHYSICS GALAXY - ASHISH ARORAChapter:NEWTONS LAWS OF MOTIONExercise:Unsolved Numerical Problem
Explore 81 Videos
Similar Questions
An isolated particle of mass m is moving in horizontal planexy along the x-axis, at a certain height above the ground. It suddenly explodes into two fragment of masses m/4 and 3m/4. An instant later, the smaller fragment is at y=+15 cm. The larger fragment at this instant is at
View SolutionIn which o the following cases the centre of mass of a rod is certainly not at its centre?
View SolutionA ball is released from rest. If it takes 1 second to cross the last 20 m before hitting the ground, find the height from which it was dropped.
View SolutionA packet of 150kg is released from an air plane travelling due east at an altitude of 7200 m with a ground speed of 100 m/s. The wind applies a constant force on the packet of 300 N directed horizontally in the opposite direction to the plane's flight path. Where and when does the packet hit the ground, (with respect to the release location and time)
View SolutionTwo bars of masses m_1 and m_2 connected by a weightless spring of stiffness k , rest on a smooth horizontal plane. Bar 2 is shifted by a small distance x_0 to the left and released. The veloicyt of the centre of mass of the system when bar 1 breaks off the wall is
View SolutionA horizontal plane supports a plank with a bar of mass m placed on it and attached by a light elastic non-deformed cord of length l_0 , to a point O. The coefficient of friciton between the bar and the plank is equal to m . The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord derivates from the vertical by an angle theta . Find the work that has been performed by the moment by the frictional force acting on the bar in the reference frame fixed to the plane.
View SolutionA small bar A resting on a smooth horizontal plane is attached by threads to a point P and by means of weightless pulley, to a weight B possessing the same mass as the bar itself. The bar is also attached to a point O by means of a light non-deformed spring of length l0=50cm and stiffness k=mg/l0, where m is the mass of the bar. The thread PA having been burned, the bar starts moving to the right. Find its velocity at the moment when it is breaking off the plane.

View SolutionTwo touching bars 1 and 2 are placed on an inclined plane forming an angle alpha with the horizontal (figure). The masses of the bars are equal to m_1 and m_2 , and the coefficients of friction between the inclined plane and these bars are equal to k_1 and k_2 respectively, with k_1gtk_2 . Find: (a) the force of interaction of the bars in the process of motion, (b) the minimum value of the angle alpha at which at bars start sliding down.
View SolutionA plank of mass m1 with a bar of mass m2 placed on it lies on a smooth horizontal plane. A horizontal force growing with time t as F′=at (a is constant) is applied to the bar. Find how the accelerations of the plank w1 and of the bar w2 depend on t, if the coefficient of friction between the plank and the bar is equal to k. Draw the approximate plots of these dependences.
View SolutionTwo bars of masses m1 and m2 connected by a non-deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to k. What minimum constant force has to be applied in the horizontal direction to the bar of mass m1 in order to shift the other bar?
View SolutionA small bar A resting on a smooth horizontal plane is attached by threads to a point P(figure) and, by means of a weightless pulley, to a weight B possessing the same mass as the bar itself.
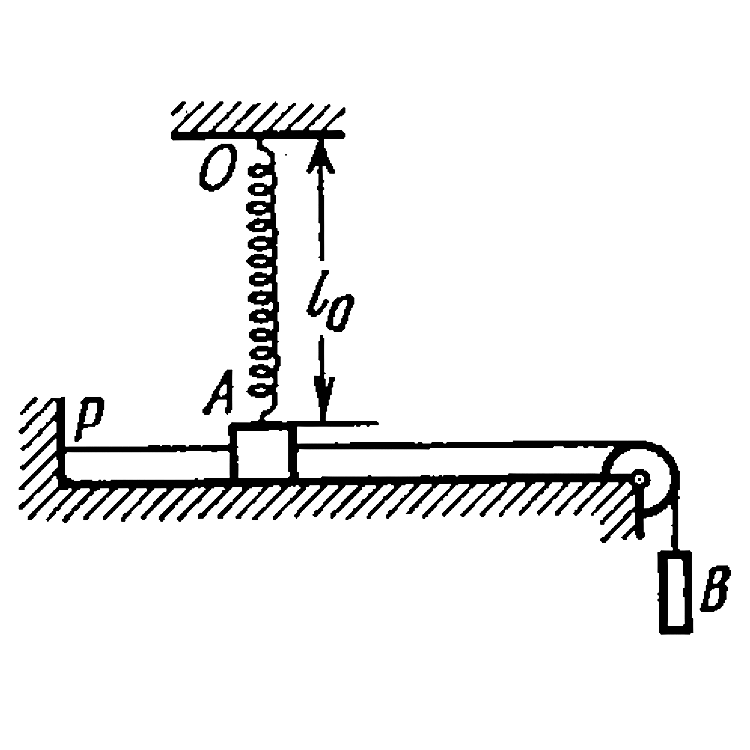
Besides, the bar is also attached to a point O by means of a light non-deformed spring of length l0=50cm and stiffness x=5mg/l0, where m is the mass of the bar. The thread PA having been burned, the bar starts moving. Find its velocity at the moment when it is breaking off the plane.
View SolutionA horizontal plane supports a plank with a bar of mass m=1.0kg placed on it and attached by a light elastic non-deformed cord of length l0=40cm to a point O(figure). The coefficient of friction between the bar and the plank equals k=0.20. The plank is slowly shifted to the right until the bar starts sliding over it. It occurs at the moment when the cord deviates from the vertical by an angle θ=30∘. Find the work that has been performed by that moment by the friction force acting on the bar in the reference frame fixed to the plane.

View SolutionTwo bars of masses m1 and m2 connected by a weightless spring of stiffness ϰ (figure) rest on a smooth horizontal plane.

Bar 2 is shifted a small distance x to the left and then released. Find the velocity of the centre of inertia of the system after bar 1 breaks off the wall.
View SolutionTwo bars connected by a weightless spring of stiffness ϰ and length (in the non-deformed state) l_0 rest on a horizontal plane. A constant horizontal force F starts acting on one of the bars as shown in figure. Find the maximum and minimum distances between the bars during the subsequent motion of the system, if the masses of the bars are: (a) equal: (b) equal to m_1 and m_2 , and the force F is applied to the bar of mass m_2 .
View SolutionA bar of mass m=0.50kg lying on a horizontal plane with a friction coefficient k=0.10 is attached to the wall by means of a horizontal non - deformed spring. The stiffness of the spring is equal to x=2.45 N//cm , its mass is negligibl . The bar was displaced so that the spring was stretched by x_(0)=3.0 cm , and then released. Find : (a) the period of oscillation of the bar , (b) the total number os osciallations that the bar performs untial it stops completely.
View SolutionTwo bars of masses m_(1) and m_(2) connected by a non - deformed light spring rest on a horizontal plane. The coefficient of friction between the bars and the surface is equal to mu . What minimum constant force has to be appled in the horizontal direction to the bar of mass m_(1) in order to shift the other bar?
View Solution

