Two balls of masses $m_{1} = 0.5 k g and m_{2} = 0.3 k g$ are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with $ω = 110$ rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if $l = 20$ cm is the length of the string. Is the equilibrium of the balls stable ?

Video Solution

Answer

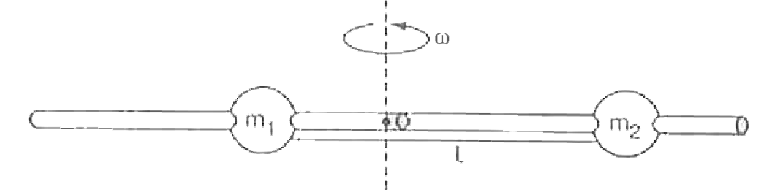
Step by step video & image solution for Two balls of masses m_(1) = 0.5 kg and m_(2) = 0.3 kg are connected by a nonstretchable string and slipped on to a horizontal , light rod. The rod is rotated with omega = 110 rpm about a vertical axis passing through its centre. Find the tension of the string and the distance of the masses from the axis of rotation if l=20 cm is the length of the string. Is the equilibrium of the balls stable ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS CIRCULAR MOTION

Topper's Solved these Questions

Knowledge Check

A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
Asame at all points
Bdifferent at differen points and maximum at centre of rod
Cdifferent at different points and minimum at axis of rotation.
Ddifferent at different points and maximum at axis of rotation
A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A $\frac{1}{2} m ω^{2} x$
B $\frac{1}{2} m ω^{2} (1 - \frac{x^{2}}{l})$
C $\frac{1}{2} m ω^{2} l (1 - \frac{x^{2}}{l^{2}})$
D $\frac{1}{2} m ω^{2} l [1 - \frac{x}{l}]$
A rod of length 2 m has a mass of 0.24 kg. Its moment of inerita about an axis passing through its centre and perpendicular to the length of the rod is
A ${0.04 kg - m}^{2}$
B ${0.08 kg - m}^{2}$
C ${0.12 kg - m}^{2}$
D ${0.02 kg - m}^{2}$

NN GHOSH-CENTRIPITAL AND CENTRIFUGAL FORCES-Exercises (B)

Home
Ask Doubt
Profile

Topper's Solved these Questions

Similar Questions

Knowledge Check

A uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is

A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is

A rod of length 2 m has a mass of 0.24 kg. Its moment of inerita about an axis passing through its centre and perpendicular to the length of the rod is

NN GHOSH-CENTRIPITAL AND CENTRIFUGAL FORCES-Exercises (B)

A uniform rod of mass $m$ and length $l$ rotates in a horizontal plane with an angular velocity $ω$ about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is